सूर्यसिद्धान्त

सूर्यसिद्धान्त के प्रथम श्लोक्क में रचनाकार ने ब्रह्म को नमस्कार करते हुए उसे अचिन्त्य, अव्यक्तरूप, निर्गुण, गुणात्मन, और समस्त जगत का आधार बताया है।

सूर्यसिद्धान्त भारतीय खगोलशास्त्र का प्रसिद्ध ग्रन्थ है। कई सिद्धान्त-ग्रन्थों के समूह का नाम है। वर्तमान समय में उपलब्ध ग्रन्थ मध्ययुग में रचित ग्रन्थ लगता है किन्तु अवश्य ही यह ग्रन्थ पुराने संस्क्रणों पर आधारित है जो ६ठी शताब्दी के आरम्भिक चरण में रचित हुए माने जाते हैं।

भारतीय गणितज्ञों और खगोलशास्त्रियों ने इसका सन्दर्भ भी लिया है, जैसे आर्यभट्ट और वाराहमिहिर, आदि. वाराहमिहिर ने अपने पंचसिद्धांतिका में चार अन्य टीकाओं सहित इसका उल्लेख किया है, जो हैं:

• पैतामाह सिद्धान्त, (जो कि परम्परागत वेदांग ज्योतिष से अधिक समान है),
• पौलिष सिद्धान्त
• रोमक सिद्धान्त (जो यूनानी खगोलशास्त्र के समान है), और
• वशिष्ठ सिद्धान्त

सूर्य सिद्धान्त नामक वर्णित कार्य, कई बार ढाला गया है। इसके प्राचीनतम उल्लेख बौद्ध काल (तीसरी शताब्दी, ई.पू) के मिलते हैं। वह कार्य, संरक्षित करके और सम्पादित किया हुआ (बर्गस द्वारा १८५८ में) मध्य काल को संकेत करता है। वाराहमिहिर का दसवीं शताब्दी के एक टीकाकार, ने सूर्य सिद्धांत से छः श्लोकों का उद्धरण किया है, जिनमें से एक भी अब इस सिद्धांत में नहीं मिलता है। वर्तमान सूर्य सिद्धांत को तब वाराहमिहिर को उपलब्ध उपलब्ध पाठ्य का सीधा वंशज माना जा सकता है। इस लेख में बर्गस द्वारा सम्पादित किया गया संस्करण ही मिल पायेगा. गुप्त काल के जो साक्ष्य हैं, उन्हें पठन करने हेतु देखें पंचसिद्धांतिका।

इसमें वे नियम दिये गये हैं, जिनके द्वारा ब्रह्माण्डीय पिण्डों की गति को उनकी वास्तविक स्थिति सहित जाना जा सकता है। यह विभिन्न तारों की स्थितियां, चांद्रीय नक्षत्रों के सिवाय; की स्थिति का भी ज्ञान कराता है। इसके द्वारा सूर्य ग्रहण का आकलन भी किया जा सकता है।

वर्ण्य विषय

सूर्य सिद्धान्त में खगोलीय समय चक्रों का विस्तृत वर्णन है।

खगोलशास्त्र

इस ग्रन्थ में विषयों की सूची निम्न है:

1. मध्यमाधिकारः -- ग्रहों की चाल
2. स्पष्टाधिकारः -- ग्रहों की स्थिति
3. त्रिप्रश्नाधिकारः -- दिशा, स्थान और समय
4. चन्द्रग्रहणाधिकारः -- चंद्रमा और ग्रहण
5. सूर्यग्रहणाधिकारः -- सूर्य और ग्रहण
6. छेद्यकाधिकारः -- ग्रहणों का पूर्व अनुमान/ आकलन
7. ग्रहयुत्यधिकारः -- ग्रहीय संयोग
8. भग्रहयुत्यधिकारः -- तारों के बारे में
9. उदयास्ताधिकारः -- उनका उदय और अस्त
10. चन्द्रशृंगोन्नत्यधिकारः -- चंद्रमा का उदय और अस्त
11. पाताधिकारः -- सूर्य और चंद्रमा के एकई अहितकर पक्ष
12. भूगोलाध्यायः -- विश्वोत्पत्ति/ब्रह्माण्ड सृजन, भूगोल और सृजन के आयाम
13. ज्यौतिषोपनिषदध्यायः -- सूर्य घड़ी का दण्ड
14. मानाध्यायः -- लोकों की गति और मानवीय क्रिया-कलाप

सौर घड़ी द्वारा समय मापन के शुद्ध तरीके अध्याय 3 और 13 में वर्णित हैं।

ग्रहों की चाल

भगण

- 12 राशियो का एक भगण होता है ।

- 60 विकला की एक कला ।

- 60 कला का - 1 अंश ।

- 30 अंश को - 1 राशी ।

- शीघ्र्‍ गति वाले ग्रह अल्पकाल मे तथा मंद गतिवाले अधिक काल मे 27 नक्षत्र का भोग करते है ।

- अश्विनी नक्षत्र सें भ्रमण करते हुये रेवती नक्षत्र तक ग्रहो का भगण पुरा होता है ।

- पुर्वाभिमुख गमन करने वाले सुर्य-बुध और शुक्र और मंगल शनि और गुरू की भगण संख्या 4320000 होती है ।

- एक महायुग मे चंद्रमा कि भगण संख्या – 57753336,

- एक महायुग मे मंगल कि भगण संख्या – 2296832,

- एक महायुग मे बुध कि भगण संख्या – 17937060,

- एक महायुग मे गुरु की भगण संख्या – 364220

- एक महायुग मे शुक्र की भगण संख्या – 7022376

- एक महायुग मे शनि की भगण संख्या – 146568

- चंद्र की भगण संख्या – 488203

- राहु-केतु की विपरीत गति से भगणों कि – 232236 संख्या होती है ।

- एक महायुग मे नक्षत्रो की भगण संख्या – 1582237828 होती है ।

- नाक्षत्र भगण मे से ग्रहो के अपने अपने भगण घटाने पर शेष ग्रहों के सावन दिन होते है

- एक महायुग मे सुर्य और चंद्रमा के भगणों के अंतर के समान चांद्रमास होते है ।

- युग चांद्रमास से युग सुर्य मास घटाने पर अधिमास मिलता है ।

- एक महायुग में 1577917828 सावन दिन होते है ।

- 1603000080 तिथियाँ होती है ।

- 1593336 आधिमास होते है ।

- 25082252 क्षय दिन होते है ।

- 51840000 सौर मास होते है ।

नक्षत्र भगण से सौर भगण घटाने पर सावन होता है ।

समय चक्र

इस ग्रंथ में वर्णित समय-चक्र विलक्षण रूप से विशुद्ध थे। हिन्दू ब्रह्माण्डीय समय चक्र सूर्य सिद्धांत के पहले अध्याय के श्लोक 11–23 में आते हैं।:

(श्लोक 11) - वह जो कि श्वास (प्राण) से आरम्भ होता है, यथार्थ कहलाता है; और वह जो त्रुटि से आरम्भ होता है, अवास्तविक कहलाता है। छः श्वास से एक विनाड़ी बनती है। साठ श्वासों से एक नाड़ी बनती है।

(श्लोक 12) - और साठ नाड़ियों से एक दिवस (दिन और रात्रि) बनते हैं। तीस दिवसों से एक मास (महीना) बनता है। एक नागरिक (सावन) मास सूर्योदयों की संख्याओं के बराबर होता है।

(श्लोक 13) - एक चंद्र मास, उतनी चंद्र तिथियों से बनता है। एक सौर मास सूर्य के राशि में प्रवेश से निश्चित होता है। बारह मास एक वरष बनाते हैं। एक वरष को देवताओं का एक दिवस कहते हैं।

(श्लोक 14) - देवताओं और दैत्यों के दिन और रात्रि पारस्परिक उलटे होते हैं। उनके छः गुणा साठ देवताओं के (दिव्य) वर्ष होते हैं। ऐसे ही दैत्यों के भी होते हैं।

(श्लोक 15) - बारह सहस्र (हज़ार) दिव्य वर्षों को एक चतुर्युग कहते हैं। एक चतुर्युग तिरालीस लाख बीस हज़ार सौर वर्षों का होता है।

(श्लोक 16) - चतुर्युगी की उषा और संध्या काल होते हैं। कॄतयुग या सतयुग और अन्य युगों का अन्तर, जैसे मापा जाता है, वह इस प्रकार है, जो कि चरणों में होता है:

(श्लोक 17) - एक चतुर्युगी का दशांश को क्रमशः चार, तीन, दो और एक से गुणा करने पर कॄतयुग और अन्य युगों की अवधि मिलती है। इन सभी का छठा भाग इनकी उषा और संध्या होता है।

(श्लोक 18) - इकहत्तर चतुर्युगी एक मन्वन्तर या एक मनु की आयु होते हैं। इसके अन्त पर संध्या होती है, जिसकी अवधि एक सतयुग के बराबर होती है और यह प्रलय होती है।

(श्लोक 19) - एक कल्प में चौदह मन्वन्तर होते हैं, अपनी संध्याओं के साथ; प्रत्येक कल्प के आरम्भ में पंद्रहवीं संध्या/उषा होती है। यह भी सतयुग के बराबर ही होती है।

(श्लोक 20) - एक कल्प में, एक हज़ार चतुर्युगी होते हैं और फ़िर एक प्रलय होती है। यह ब्रह्मा का एक दिन होता है। इसके बाद इतनी ही लम्बी रात्रि भी होती है।

(श्लोक 21) - इस दिन और रात्रि के आकलन से उनकी आयु एक सौ वर्ष होती है; उनकी आधी आयु निकल चुकी है और शेष में से यह प्रथम कल्प है।

(श्लोक 22) - इस कल्प में, छः मनु अपनी संध्याओं समेत निकल चुके, अब सातवें मनु (वैवस्वत: विवस्वान (सूर्य) के पुत्र) का सत्तैसवां चतुर्युगी बीत चुका है।

(श्लोक 23) - वर्तमान में, अट्ठाईसवां चतुर्युगी का कॄतयुग बीत चुका है।........

इस खगोलीय समय चक्र का आकलन करने पर, निम्न परिणाम मिलते हैं

• उष्णकटिबनधीय वर्ष की औसत लम्बाई है 365.2421756 दिवस, जो कि आधुनिक आकलन से केवल 1.4 सैकण्ड ही छोटी है। (J2000). यह उष्णकटिबन्धीय वर्ष का सर्वाधिक विशुद्ध आकलन रहा कम से कम अगली छः शताब्दियों तक, जब मुस्लिम गणितज्ञ उमर खय्याम ने एक बेहतर अनुमान दिया. फ़िर भी यहआकलन अभी भी विश्व में प्रचलित ग्रेगोरियन वर्ष के मापन से अति शुद्ध ही है, जो कि वर्शः की अवधि केवल 365.2425 दिवस ही बताता है, यथार्थ 365.2421756 दिवस के स्थान पर.

• एक नाक्षत्रीय वर्ष की औसत अवधि, पृथ्वी के द्वारा, सूर्य की परिक्रमा में लगे समय अवधि 365.2563627 दिवस होती है, जो कि आधुनिक मान 365.25636305 दिवस (J2000) के एकदम बराबर ही है। यह नाक्षत्रीय वर्ष का सर्वाधिक परिशुद्ध कलन यहा सहस्रों वर्ष तक.

नाक्षत्रीय वर्ष का दिया गया यथार्थ मान, वैसे उतना शुद्ध नहीं है। इसका मान 365.258756 दिवस दिया गया है, जो कि आधुनिक मान से 3 मिनट और 27 सैकण्ड कम है। यह इसलिये है, क्योंकि लेखक, या सम्पादक ने बाद में किये गये कलनों में हिन्दू ब्रह्माण्डीय समय चह्र की गणना से थोड़ा भिन्न हो कर यहां गणना की है। उसने शायद समय चक्र के जटिल गणना के आकलन को सही समझा नहीं है। सम्पादक ने सूर्य की औसत गति और समान परिशुद्धता का प्रयोग किया है, जो कि हिन्दू ब्रह्माण्डीय समय चक्र के आकलन से निम्न स्तर का है।

पृथ्वी गोल है

सर्वत्रैव महीगोले स्वस्थानम् उपरि स्थितम् ।

मन्यन्ते खे यतो गोलस् तस्य क्वोर्धवम् क्व वाधः ॥ (सूर्यसिद्धान्त १२.५३)

अनुवाद : (अनुवादक: स्कॉट एल मॉण्टगोमरी, आलोक कुमार) इस गोलाकार धरती पर लोग अपने स्थान को सबसे ऊपर मानते हैं। किन्तु यह गोला तो आकाश में स्थित है, उसका उर्ध्व (ऊपर) क्या और नीचे क्या?

ग्रहों के व्यास

सूर्य सिद्धान्त में ग्रहों के व्यास की गणना भी की गयी है। बुध का व्यास ३००८ मील दिया गया है जो आधुनिक स्वीकृत मान (३०३२ मील्) से केवल १% कम है। इसके अलावा शनि, मंगल, शुक्र और बृहस्पति के व्यास की गणना भी की गयी है। शनि का व्यास ७३८८२ मील बताया गया है जो केवल १% अशुद्ध है। मंगल का व्यास ३७७२ मील बताया गया है जो लगभग ११% अशुद्ध है। शुक्र का व्यास ४०११ मील तथा बृहस्पति का व्यास ४१६२४ मील बताया गया है जो वर्तमान स्वीकृत मानों के लगभग आधे हैं।

त्रिकोणमिति

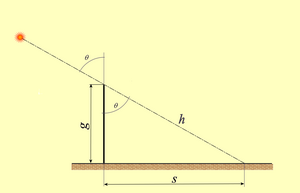
सूर्यसिद्धान्त आधुनिक त्रिकोणमिति का मूल है। सूर्यसिद्धान्त में वर्णित ज्या और कोटिज्या फलनों से ही आधुनिक साइन (sine) और कोसाइन (cosine) नाम व्युत्पन्न हुए हैं ( जो भारत से अरब-जगत होते हुए यूरोप पहुँचे)। इतना ही नहीं, सूर्यसिद्धान्त के तृतीय अध्याय (त्रिप्रश्नाधिकारः) में ही सबसे पहले स्पर्शज्या (tangent) और व्युकोज्या (secant) का प्रयोग हुआ है। निम्नलिखित श्लोकों में शंकुक द्वारा निर्मित छाया का वर्णन करते हुए इनका उपयोग हुआ है-

शेषम् नताम्शाः सूर्यस्य तद्बाहुज्या च कोटिज्या।

शंकुमानांगुलाभ्यस्ते भुजत्रिज्ये यथाक्रमम् ॥ ३.२१ ॥

कोटिज्यया विभज्याप्ते छायाकर्णाव् अहर्दले।

क्रान्तिज्या विषुवत्कर्णगुणाप्ता शंकुजीवया ॥ ३.२२ ॥

Of [the sun's meridian zenith distance] find the jya ("base sine") and kojya (cosine or "perpendicular sine"). If then the jya and radius be multiplied respectively by the measure of the gnomon in digits, and divided by the kojya, the results are the shadow and hypotenuse at mid-day.

उपरोक्त सूत्र से, आधुनिक प्रतीकों का उपयोग करते हुए, दोपहर के समय शंकुक (gnomon) की छाया की लम्बाई यह होगी-

<math>s = \frac{g \sin \theta}{\cos \theta} = g \tan \theta</math>

तथा, दोपहर के समय, शंकुक के विकर्ण (hypotenuse) की लम्बाई यह होगी-

<math>h = \frac{g r}{\cos \theta} = g r \frac{1}{\cos \theta} = g r \sec \theta</math>

जहाँ <math>\ g</math> शंकुक की लम्बाई (उंचाई) है, <math>\ r</math> शंकुक की त्रिज्या है, <math>\ s</math> शंकुक की छाया की लम्बैइ है, और <math>\ h</math> शंकुक का विकर्ण है।

कैलेण्डरीय प्रयोग

१८७१-७२ ई का हिन्दू पञ्चाङ्ग

भारत के विभिन्न भागों में भारतीय सौर पंचांग तथा चन्द्र-सौर पंचांग प्रयुक्त होते हैं। इनके आधार पर ही विभिन्न त्यौहार, मेले, क्रियाकर्म होते हैं। भारत में प्रचलित आधुनिक सौर तथा चान्द्रसौर पंचांग, सूर्य के विभिन्न राशियों में प्रवेश के समय पर ही आधारित हैं।

परम्परागत पंचांगकार, आज भी सूर्यसिद्धान्त में निहित सूत्रों और समीकरणों का ही प्रयोग करके अपने पंचांग का निर्माण करते हैं। भारतीयों के धार्मिक एवं सामाजिक जीवन पर पंचांग का बहुत अधिक प्रभाव है तथा अधिकांश घरों में पंचांग रखने की प्रथा है।

यंत्र

पारदाराम्बुसूत्राणि शुल्वतैलजलानि च।

बीजानि पांसवस्तेषु प्रयोगास्तेऽपि दुर्लभाः ॥१३.२२ ॥

अर्थ : ताड़ियों (spokes) में पारद भरा हुआ, जल, धागा (सूत्र), रस्सी, तेल और जल आदि से ये यंत्र बनाये जाते हैं। इसके अलावा बीज और महीन रेत भी इन यंत्रों में प्रयुक्त होती हैं। ये यन्त्र दुर्लभ हैं।

अनुवाद एवं व्याख्या

• Translation of the Sûrya-Siddhânta: A text-book of Hindu astronomy, with notes and an appendix by Ebenezer Burgess Originally published: Journal of the American Oriental Society 6 (1860) 141–498. Commentary by Burgess is much larger than his translation.

• बापू देव शास्त्री कृत सूर्यसिद्धान्त का अनुवाद (1861) ISBN 3-7648-1334-2, ISBN 978-3-7648-1334-5. Only a few notes। Translation of Surya Siddhanta occupies first 100 pages; rest is a translation of the Siddhanta Siromani by Lancelot Wilkinson.

• Surya-Siddhanta: A Text Book of Hindu Astronomy by Ebenezer Burgess, ed. Phanindralal Gangooly (1989/1997) with a 45-page commentary by P. C. Sengupta (1935).

सन्दर्भ

• Ebenezer Burgess. "Translation of the Surya-Siddhanta, a text-book of Hindu Astronomy", Journal of the American Oriental Society 6 (1860): 141–498.
• Victor J. Katz. A History of Mathematics: An Introduction, 1998.
• Dwight William Johnson. Exegesis of Hindu Cosmological Time Cycles, 2003.

देखें

• हिन्दू समय चक्र
• भारतीय विज्ञान और प्रौद्योगिकी
• भारतीय गणित
• हिन्दू खगोलशास्त्र
• वेदांग ज्योतिष

बाहरी कड़ियाँ

• सूर्यसिद्धान्त (संस्कृत विकिस्रोत)
• सूर्यसिद्धान्त (देवनागरी पाठ)
• सूर्यसिद्धान्त (देवनागरी पाठ)
• सूर्यसिद्धान्त (राष्ट्रीय संस्कृत संस्थान)
• सूर्यसिद्धान्त का हिन्दी अनुवाद (प्रथम चार अध्याय)
• सूर्य सिद्धान्त का अनुवाद
• Surya-Siddhanta: A Text Book of Hindu Astronomy (1858) by Ebenezer Burgess Kessinger Publishing
• Surya-Siddhanta: A Text Book of Hindu Astronomy by Ebenezer Burgess Phanindralal Gangooly
• Surya-Siddhanta: A Text Book of Hindu Astronomy; With Notes and an Appendix by Ebenezer Burgess JSTOR
• Surya Siddhanta Sanskrit text in Devanagari.
• Surya Siddhanta. PDF scans of various (English and Sanskrit) editions, with and without Sansksrit commentaries. (English, Sanskrit)