त्रिभुज

त्रिभुज (Triangle), तीन शीर्षों और तीन भुजाओं (side) वाला एक बहुभुज (Polygon) होता है। यह ज्यामिति की मूल आकृतियों में से एक है। शीर्षों A, B, और C वाले त्रिभुज को <math> \triangle ABC</math> लिखा/कहा जाता है। यूक्लिडियन ज्यामिति में कोई भी तीन असंरेखीय बिन्दु, एक अद्वितीय त्रिभुज का निर्धारण करते हैं और साथ ही, एक अद्वितीय तल (यानी एक द्वि-विमीय यूक्लिडियन समतल) का भी। दूसरे शब्दों में, तीन रेखाखण्डो से घिरी बंद आकृति को त्रिभुज या त्रिकोण कहते हैं। त्रिभुज में तीन भुजाएं और तीन कोण होते हैं। त्रिभुज सबसे कम भुजाओं वाला बहुभुज है। किसी त्रिभुज के तीनों आन्तरिक कोणों का योग सदैव 180° होता है। इन भुजाओं और कोणों के माप के आधार पर त्रिभुज का विभिन्न प्रकार से वर्गीकरण किया जाता है। दो समान्तर रेखाओ के मध्य एक ही आधार पर बने त्रिभुजो का क्षेत्रफल बराबर होता है

त्रिभुज
प्रकार	बहुभुज
भुजाएँ	AB, BC, CA या c, a, b
शीर्ष	A, B, C
कोण	∠ABC, ∠BCA, ∠BAC या ∠CAB
आन्तरिक कोणों का योग	(∠ABC + ∠BCA + ∠BAC) = 180०

त्रिभुज

कुछ परिभाषाएँ

समबाहु त्रिभुज: वह त्रिभुज जिसमें तीनों भुजाएं समान होती हैं और प्रत्येक कोण 60° का होता है।

अभिलम्ब: किसी त्रिभुज में एक भुजा के विपरीत शीर्ष से भुजा पर डाला गया लम्ब अभिलम्ब कहलाता है।

माध्यिका: शीर्ष के सामने वाली भुजा के मध्य बिन्दु से मिलाने वाली रेखा मध्यिका कहलाती है।

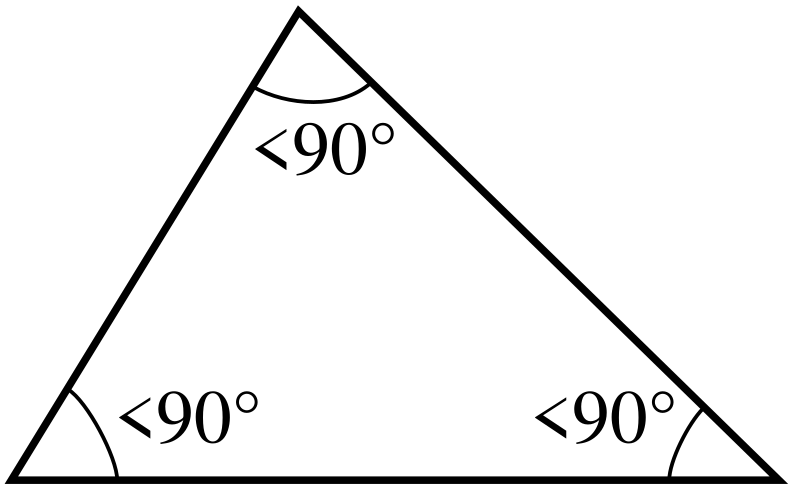
न्यूनकोण त्रिभुज: वह त्रिभुज जिसमें प्रत्येक कोण 90 डिग्री से कम होता है।

समकोण त्रिभुज: एक कोण 90 डिग्री शेष दोनों कोण एक दूसरे के पूरक होते हैं।

अधिककोण त्रिभुज: कोई भी एक कोण 90 डिग्री से अधिक का होता है।

विषमबाहु त्रिभुज: सभी भुजाएं आपस में असमान होती हैं।

समद्विबाहु त्रिभुज: कोई दो भुजाएं आपस में समान होती हैं। समान भुजाओं के सामने के कोण भी समान होते हैं।

कोण समद्विभाजक: वह रेखाखंड, जो त्रिभुज के शीर्ष से प्रारंभ होता है एवं कोण को दो समान भागों में बांटता है।

भुजा का लम्ब समद्विभाजक: रेखाखण्ड, जो त्रिभुज की भुजा के साथ समकोण बनाते हुए उसे दो समान भागों में बांटता है।

लम्ब केन्द्र: वह बिन्दु जहाँ किसी त्रिभुज के तीनों अभिलम्ब मिलते है।

केन्द्रक: त्रिभुज की तीनों मध्यिकायें जिस बिंदु पर मिलती हैं वह बिन्दु केंद्रक (सेन्ट्रॉड) कहलाता है। केंद्रक प्रत्येक मध्यिका को 2:1 में विभाजित करता है।

अंतःकेन्द्र: त्रिभुज के कोण समद्विभाजक जिस बिन्दु पर मिलते हैं, वह बिन्दु अंतःकेन्द्र कहलाता है।

परिकेन्द्र: वह बिन्दु जहाँ भुजाओं के लम्ब समद्विभाजक मिलते हैं परिकेंद्र कहलाता है। परिकेंद्र हमेशा तीनों शीर्षो से समान दूरी पर होता है।

त्रिभुजों के प्रकार

भुजाओं और कोणों के माप के आधार पर त्रिभुज का विभिन्न प्रकार से वर्गीकरण किया गया है-

भुजाओं (की लम्बाइयों) के आधार पर

समबाहु त्रिभुज (Equilateral Triangle) - एक समबाहु त्रिभुज में, सभी (तीनों) भुजाओं की लंबाई बराबर होती है। एक समबाहु त्रिभुज, एक नियमित बहुभुज भी है जिसमें सभी (तीनों) कोण 60° के होते हैं।

समद्विबाहु त्रिभुज (Isosceles Triangle) - यदि किसी त्रिभुज की कोई दो भुजाएं बराबर होती हैं तो वो समद्विबाहु त्रिभुज कहलाता है। समद्विबाहु त्रिभुज के समान भुजाओं के आमने सामने के कोण भी बराबर होते हैं। एक समद्विबाहु त्रिभुज में, किन्ही दो भुजाओं की लंबाई बराबर होती है। एक समद्विबाहु त्रिभुज में एक ही माप के दो कोण भी होते हैं, अर्थात् समान लंबाई की दोनों भुजाओं और तीसरी असमान भुजा के मध्य बने कोण समान होते हैं; यह तथ्य समद्विबाहु त्रिभुज प्रमेय का है, जिसे यूक्लिड द्वारा ज्ञात किया गया था। समद्विबाहु त्रिभुज में कम से कम दो भुजाएँ समान होती हैं। अतः समबाहु त्रिभुज, समद्विबाहु भी होते हैं।

विषमबाहु त्रिभुज (Scalene Triangle) - एक विषमबाहु त्रिभुज में, तीनों भुजाओं की लंबाई अलग अलग होती है। फलस्वरूप, इसके तीनों कोण भी अलग अलग होते हैं।

समबाहु त्रिभुज	समद्विबाहु त्रिभुज	विषमबाहु त्रिभुज

आन्तरिक कोणों की माप के आधार पर

समकोण त्रिभुज(Right-Angled Triangle)- समकोण त्रिभुज (जिसे एक आयताकार त्रिभुज भी कहा जाता है) में आंतरिक कोणों में से एक 90° (समकोण) होता है। ऐसे त्रिभुज में, समकोण के सामने की भुजा को कर्ण (hypotenuse) कहते हैं, जो त्रिभुज की सबसे लंबी भुजा होती है। अन्य दो भुजाओं को त्रिभुज के पाद (legs) या भुज (cathetus) कहा जाता है। समकोण त्रिभुज, पाइथागोरियन प्रमेय का पालन करते हैं: दो भुजों (आधार और लम्ब) की लंबाई के वर्गों का योग, कर्ण की लंबाई के वर्ग के बराबर होता है: , जहां a और b भुजों की लंबाई और c कर्ण की लंबाई है। विशेष समकोण त्रिभुज, अतिरिक्त गुणों वाले समकोण त्रिभुज होते हैं जो गणना को आसान बनाते हैं। दो सबसे प्रसिद्ध समकोण त्रिभुजों में से एक 3-4-5 समकोण त्रिभुज है, जहां <math>3^2 + 4^2 = 5^2</math>. इस स्थिति में, 3, 4, और 5 एक पाइथागोरियन युग्म है। दूसरा एक समद्विबाहु त्रिभुज है जिसमें दो कोण 45° के होते हैं।

त्रिभुजों के के प्रकार का यूलर आरेख। समद्विबाहु त्रिभुज में कम से कम दो भुजाएँ समान होती हैं। अतः समबाहु त्रिभुज, समद्विबाहु भी होते हैं।

न्यूनकोण त्रिभुज(Acute Triangle)- न्यूनकोण त्रिभुज में प्रत्येक आंतरिक कोण 90° से कम होता है। यदि c, त्रिभुज की सबसे लंबी भुजा की लंबाई है, तो <math>a^2 + b^2> c^2</math>, जहां a और b, त्रिभुज की अन्य दो भुजाओं की लंबाई हैं।

अधिककोण त्रिभुज(Obtuse Triangle)- अधिककोण त्रिभुज में, कोई एक आंतरिक कोण 90° से अधिक होता है। यदि c, त्रिभुज की सबसे लंबी भुजा की लंबाई है, तो <math>a^2 + b^2 < c^2</math>, जहां a और b, त्रिभुज की अन्य दो भुजाओं की लंबाई हैं।

समकोण त्रिभुज	अधिककोण त्रिभुज	न्यूनकोण त्रिभुज
	<math>\underbrace{\qquad \qquad \qquad \qquad \qquad \qquad}_{}</math>
	परोक्ष

मूलभूत तथ्य

यूक्लिडियन तल में, त्रिभुज के तीनों आंतरिक कोणों का योग हमेशा 180 अंश होता है। यह तथ्य यूक्लिड के समांतर स्वसिद्ध के समान है। यह किसी भी त्रिभुज के तीसरे कोण की माप का निर्धारण करने की अनुमति देता है, जब त्रिभुज के अन्य दोनों कोणों की माप ज्ञात हो। त्रिभुज का बहिष्कोण (Exterior Angle) वह कोण है जो एक आंतरिक कोण के लिए, एक रैखिक कोण (और इसलिए पूरक) होता है, अर्थात त्रिभुज की किसी भुजा को आगे बढ़ाने पर जो कोण बनता है, वह त्रिभुज का एक बहिष्कोण होता है। त्रिभुज के बहिष्कोण की माप, अन्य दो आंतरिक कोणों की मापों के बराबर होती है जो इससे संलग्न नहीं होते हैं; यह बहिष्कोण प्रमेय है। किसी भी त्रिभुज के तीनों बहिष्कोणों (प्रत्येक शीर्ष के लिए एक) की मापों का योग 360 अंश होता है।

एक त्रिभुज, जिसमें d एक बहिष्कोण है।

त्रिभुज के तीनों आंतरिक कोणों का योग हमेशा 180 अंश होता है। (समान रंग यह इंगित करता है कि वे कोण बराबर हैं)।

समरूपता और सर्वांगसमता

दो त्रिभुज समरूप (Similiar) होते हैं यदि एक त्रिभुज के प्रत्येक कोण का मान, दूसरे त्रिभुज के (तत्स्थानिक) कोणों के मान के बराबर होता है। समरूप त्रिभुजों में तत्स्थानिक भुजाओं की लंबाइयाँ समान अनुपात में होती हैं, और यह गुण त्रिभुजों में समरूपता स्थापित करने के लिए पर्याप्त है।

समरूप त्रिभुजों के बारे में कुछ मूल प्रमेय निम्न हैं:

• यदि दो त्रिभुजों के आंतरिक कोणों का एक युग्म(जोड़ा), एक दूसरे के समान होता है, और एक और युग्म भी एक दूसरे के समान होता है, तो दोनों त्रिभुज समरूप होते हैं।

• यदि दो त्रिभुजों की तत्स्थानिक भुजाओं का एक युग्म(जोड़ा), एक अन्य तत्स्थानिक भुजाओं के युग्म के समानुपाती होता है और उन भुजाओं के द्वारा निर्मित कोण भी समान होते हैं, तो दोनों त्रिभुज समरूप होते हैं। (बहुभुज की किन्हीं दो भुजाओं द्वारा निर्मित कोण, उन दोनों भुजाओं के बीच का आंतरिक कोण होता है।)

• यदि दो त्रिभुजों की तत्स्थानिक भुजाओं के तीनों युग्म समान अनुपात में होते हैं, तो दोनों त्रिभुज समरूप होते हैं।

दो त्रिभुज सर्वांगसम (Congruent) होते हैं, यदि उनकी आकृति और आकार बिल्कुल एक जैसे हों, दोनों त्रिभुजों में आंतरिक कोण के सभी जोड़े माप में बराबर हों, और तीनों तत्स्थानिक भुजाओं की लंबाई समान हो।

दो त्रिभुजों के सर्वांगसम होने के लिए, कुछ अलग-अलग आवश्यकताएँ और पर्याप्त स्थितियां निम्न हैं:

• SAS (Side-Angle-Side) नियम: एक त्रिभुज में किन्हीं दो भुजाओं की लंबाई, दूसरे त्रिभुज में किन्हीं दो भुजाओं की लंबाई के बराबर होती है, और एक कोण की माप भी समान होती है।

इसी प्रकार, दो त्रिभुजों की सर्वांगसमता सिद्ध करने के लिए ASA नियम, SSS नियम, AAS नियम का प्रयोग किया जाता है।

समकोण त्रिभुज

पाइथागोरियन प्रमेय

समकोण त्रिभुज (जिसे एक आयताकार त्रिभुज भी कहा जाता है) में आंतरिक कोणों में से एक 90° (समकोण) होता है। ऐसे त्रिभुज में, समकोण के सामने की भुजा को कर्ण कहते हैं, जो त्रिभुज की सबसे लंबी भुजा होती है। अन्य दो भुजाओं को त्रिभुज के पाद (legs) या भुज (cathetus) कहा जाता है। पाइथागोरियन प्रमेय एक केंद्रीय प्रमेय है, जो कि किसी भी समकोण त्रिभुज में लागू हो सकती है: कर्ण की लंबाई का वर्ग,अन्य दो भुजाओं की लंबाई के वर्गों के योग के बराबर होता है। यदि कर्ण की लंबाई c, और भुजों की लंबाइयाँ a और b है, तो प्रमेय के अनुसार-

<math>{\displaystyle a^{2}+b^{2}=c^{2}.}</math>

अर्थात यदि त्रिभुज की भुजाओं की लम्बाई उपरोक्त समीकरण को संतुष्ट करती हैं, तो त्रिभुज में एक समकोण है जो भुजा c के सम्मुख है।

समकोण त्रिभुजों के बारे में कुछ अन्य तथ्य:

एक समकोण त्रिभुज के न्यूनकोण पूरक होते हैं।

<math>{\displaystyle a+b+90^{\circ }=180^{\circ }\Rightarrow a+b=90^{\circ }\Rightarrow a=90^{\circ }-b.}</math>

यदि समकोण त्रिभुज के भुजों (कर्ण के अलावा अन्य दो भुजाएँ) की लंबाई समान है, तो उन भुजों के विपरीत (या सम्मुख) कोण समान होते हैं। चूंकि ये कोण पूरक होते हैं, अतः प्रत्येक कोण 45 अंश का होता है। पाइथागोरियन प्रमेय द्वारा, कर्ण की लंबाई, एक भुज की लंबाई की √2 गुनी होती है।

30 और 60 अंश के न्यूनकोण वाले समकोण त्रिभुज में, कर्ण की लंबाई, छोटी भुजा की लंबाई की दोगुनी होती है, और बड़ी भुजा की लंबाई छोटी भुजा की लंबाई की √3 गुना होती है:

<math>c=2a\,</math>

<math>b=a\times {\sqrt {3}}.</math>

सभी त्रिभुजों के लिए कोण और भुजाएँ, ज्या(Sine) और कोज्या(Cosine) के नियमों द्वारा संबंधित हैं।

त्रिभुज का अस्तित्व

भुजाओं की शर्तें

त्रिभुज असमिका(Triangle Inequality) बताती है कि त्रिभुज की किन्हीं दो भुजाओं की लम्बाइयों का योग, तीसरी भुजा की लंबाई से अधिक या बराबर होना चाहिए। केवल एक पतित त्रिभुज में, किन्हीं दो भुजाओं की लम्बाइयों का योग, तीसरी भुजा की लंबाई के बराबर होता है, जिसमें तीनों शीर्ष संरेखीय होते हैं। त्रिभुज की दो भुजाओं की लम्बाइयों के योग का, तीसरी भुजा की लंबाई से कम होना संभव नहीं है। तीन दी गईं सकारात्मक भुजाओं वाला त्रिभुज बनेगा यदि वे भुजाएँ, त्रिभुज असमिका को संतुष्ट करती हैं।

कोणों पर शर्तें

तीन दिए गए कोण एक अपतित त्रिभुज बनाते हैं यदि वे इन दोनों शर्तों का पालन करते हैं: (a) कोणों में से प्रत्येक सकारात्मक हो, और (b) कोणों का योग 180° के बराबर है। पतित त्रिभुजों के लिए कोण 0° का हो सकता है।

त्रिकोणमितीय शर्तें

तीन सकारात्मक(Positive) कोण α, β, और γ (इनमें से प्रत्येक 180° से कम है), एक त्रिभुज के कोण होंगे यदि वे निम्न शर्तों में से किसी एक का पालन करें:

<math>\tan {\frac {\alpha }{2}}\tan {\frac {\beta }{2}}+\tan {\frac {\beta }{2}}\tan {\frac {\gamma }{2}}+\tan {\frac {\gamma }{2}}\tan {\frac {\alpha }{2}}=1,</math>

<math>\sin ^{2}{\frac {\alpha }{2}}+\sin ^{2}{\frac {\beta }{2}}+\sin ^{2}{\frac {\gamma }{2}}+2\sin {\frac {\alpha }{2}}\sin {\frac {\beta }{2}}\sin {\frac {\gamma }{2}}=1,</math>

<math>\sin(2\alpha )+\sin(2\beta )+\sin(2\gamma )=4\sin(\alpha )\sin(\beta )\sin(\gamma ),</math>

<math>\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma +2\cos(\alpha )\cos(\beta )\cos(\gamma )=1,</math>

<math>\tan(\alpha )+\tan(\beta )+\tan(\gamma )=\tan(\alpha )\tan(\beta )\tan(\gamma ),</math>

अंतिम समानता केवल तभी लागू होती है जब कोणों में से कोई भी 90° का न हो (इसलिए स्पर्शज्या फलन का मान हमेशा सीमित होता है)।

त्रिभुज से संबन्धित बिन्दु, रेखाएं, और वृत्त

त्रिभुज के तीन लंब समद्विभाजक होते हैं, जो एक ही बिंदु पर मिलते हैं (या प्रतिच्छेद करते हैं)। यह बिन्दु त्रिभुज का 'परिकेन्द्र' कहलाता है। यह बिंदु त्रिभुज के परिवृत्त का केंद्र होता है (यह वृत्त त्रिभुज के तीनों शीर्षों से होकर गुजरता है)।

एक त्रिभुज की किसी भुजा का लंब समद्विभाजक (Perpendicula Bisector), उस भुजा के मध्यबिन्दु से गुजरने वाली एक सीधी रेखा है जो भुजा के लम्बवत होती है, यानी भुजा के साथ समकोण बनाती है। त्रिभुज के तीन लंब समद्विभाजक होते हैं, जो एक ही बिंदु पर मिलते हैं (या प्रतिच्छेद करते हैं)। यह बिन्दु त्रिभुज का 'परिकेन्द्र (Circumcenter)' कहलाता है, इसे आमतौर पर O द्वारा दर्शाया जाता है; यह बिंदु त्रिभुज के परिवृत्त(Circumcircle) का केंद्र होता है (यह वृत्त त्रिभुज के तीनों शीर्षों से होकर गुजरता है)। इस वृत्त का व्यास, जिसे परिव्यास (Circumdiameter) कहा जाता है, उपरोक्त ज्या के नियम द्वारा ज्ञात किया जा सकता है। परिवृत्त की त्रिज्या को परित्रिज्या (Circumradius) कहा जाता है।

थाल्स प्रमेय से पता चलता है कि यदि परिकेन्द्र, त्रिभुज की किसी भुजा पर स्थित है, तो वह त्रिभुज समकोण त्रिभुज है और उस भुजा के सामने का कोण समकोण है। यदि परिकेन्द्र, त्रिभुज के अंदर स्थित है, तो त्रिभुज न्यूनकोण त्रिभुज है; यदि परिकेन्द्र, त्रिभुज के बाहर स्थित है, तो त्रिभुज अधिककोण त्रिभुज है।

त्रिभुज के तीन शीर्षलंब होते हैं, जो एक ही बिंदु पर प्रतिच्छेद करते हैं। यह बिन्दु त्रिभुज का 'लंबकेंद्र' कहलाता है,

त्रिभुज का शीर्षलंब (Altitude), एक शीर्ष से होकर जाने वाली एक सीधी रेखा है, जो उस शीर्ष के सामने की भुजा पर लंब होती है। इस सामने की भुजा को, शीर्षलंब का आधार (Base of the altitude) कहा जाता है, और वह बिंदु जहां शीर्षलंब, आधार को प्रतिच्छेद करता है, शीर्षलंब का पाद (Foot of the altitude) कहलाता है। शीर्षलंब की लंबाई, आधार और शीर्ष के बीच की दूरी है। त्रिभुज के तीन शीर्षलंब होते हैं, जो एक ही बिंदु पर मिलते हैं (या प्रतिच्छेद करते हैं)। यह बिन्दु त्रिभुज का 'लंबकेंद्र (Orthocenter)' कहलाता है, जो H द्वारा दर्शाया जाता है। केवल न्यूनकोण त्रिभुजों में, लंबकेंद्र त्रिभुज के अंदर स्थित होता है।

त्रिभुज के तीन कोण समद्विभाजक होते हैं, जो एक ही बिंदु पर मिलते हैं (या प्रतिच्छेद करते हैं)। यह बिन्दु त्रिभुज का 'अन्तःकेंद्र' कहलाता है।

त्रिभुज का कोण समद्विभाजक (Angle Bisector), शीर्ष से होकर जाने वाली एक सीधी रेखा है, जो उस शीर्ष के कोण को दो समान भागों में बाँटती है। त्रिभुज के तीन कोण समद्विभाजक होते हैं, जो एक ही बिंदु पर मिलते हैं (या प्रतिच्छेद करते हैं)। यह बिन्दु त्रिभुज का 'अन्तःकेंद्र (Incenter)' कहलाता है, इसे आमतौर पर I द्वारा दर्शाया जाता है; यह बिंदु त्रिभुज के अन्तःवृत्त (Incircle) का केंद्र होता है (यह वृत्त त्रिभुज के अंदर स्थित होता है और उसकी तीनों भुजाओं को स्पर्श करता है)। अन्तःवृत्त की त्रिज्या को अन्तःत्रिज्या (Inradius) कहा जाता है। किसी त्रिभुज के तीन बहिर्वृत्त (excircle या escribed circle) होते हैं। ये तीनों वृत्त उस त्रिभुज के बाहर होते हैं। इनमें से प्रत्येक वृत्त, त्रिभुज की किसी एक भुजा को तथा शेष दो भुजाओं को आगे बढाने से बनी दो रेखाओं को स्पर्श करता है।

ज की तीन माध्यिकाएँ होती हैं, जो एक ही बिंदु पर मिलती हैं (या प्रतिच्छेद करती हैं)। यह बिन्दु त्रिभुज का 'केंद्रक' कहलाता है।

त्रिभुज की माध्यिका (Median), एक शीर्ष और उस शीर्ष के सामने की भुजा के मध्यबिंदु से होकर जाने वाली एक सीधी रेखा है। माध्यिका, त्रिभुज को दो बराबर क्षेत्रों में विभाजित करती है। त्रिभुज की तीन माध्यिकाएँ होती हैं, जो एक ही बिंदु पर मिलती हैं (या प्रतिच्छेद करती हैं)। यह बिन्दु त्रिभुज का 'केंद्रक (Centroid)' कहलाता है, जो G द्वारा दर्शाया जाता है। एक दृढ़ त्रिभुजाकार वस्तु (जो एकसमान घनत्व की पतली शीट से काटा गया है) का केंद्र, उसका द्रव्यमान केंद्र (Center of Mass) भी होता है: एकसमान गुरुत्वाकर्षण क्षेत्र में, वस्तु अपने केंद्रक पर संतुलित रह सकती है। केंद्रक, प्रत्येक माध्यिका को 2:1 के अनुपात में विभाजित करता है, यानी एक शीर्ष और केंद्रक के बीच की दूरी, केंद्रक और सामने की भुजा के मध्यबिंदु के बीच की दूरी से दोगुनी होती है।

तीनों भुजाओं के मध्य बिंदु और तीनों शीर्षलम्बों के पाद, सभी एक ही वृत्त पर होते हैं, जिसे त्रिभुज का नवबिन्दु वृत्त कहते हैं।

तीनों भुजाओं के मध्य बिंदु और तीनों शीर्षलम्बों के पाद, सभी एक ही वृत्त पर होते हैं, जिसे त्रिभुज का नवबिन्दु वृत्त (Nine-point Circle) कहते हैं। शेष तीन बिंदु जिनके लिए इसका नाम नवबिन्दु (नौ बिन्दु) वृत्त है, वे शीर्ष और लंबकेन्द्र के बीच, शीर्षलंब के हिस्से के मध्यबिंदु हैं। नवबिन्दु वृत्त की त्रिज्या, परिवृत्त की त्रिज्या की आधी होती है। यह अन्तःवृत्त और तीनों बहिर्वृत्तों को स्पर्श करता है।

यूलर रेखा वह रेखा है, जिस पर केंद्रक (पीला), लंबकेन्द्र (नीला), परिकेन्द्र (हरा) और नवबिन्दु वृत्त का केंद्र (लाल बिंदु) स्थित होते हैं।

केंद्रक (पीला), लंबकेन्द्र (नीला), परिकेन्द्र (हरा) और नवबिन्दु वृत्त का केंद्र (लाल बिंदु), सभी एक एकल रेखा पर होते हैं, जिसे यूलर की रेखा (लाल रेखा) कहा जाता है। नवबिन्दु वृत्त का केंद्र, लंबकेन्द्र और परिकेन्द्र के बीच के मध्यबिंदु पर स्थित होता है, और केंद्रक और परिकेन्द्र के बीच की दूरी, केंद्रक और लंबकेन्द्र के बीच की दूरी की आधी होती है।

अन्तःवृत्त का केंद्र, सामान्य रूप से यूलर की रेखा पर स्थित नहीं होता है।

भुजाओं और कोणों की गणना

त्रिभुज में, भुजा की लंबाई या कोण की माप की गणना करने के लिए विभिन्न मानक विधियां हैं। समकोण त्रिभुज में इनके मानों की गणना करने के लिए कुछ विधियां उपयुक्त हैं; लेकिन अन्य परिस्थितियों में अधिक जटिल विधियों की आवश्यकता हो सकती है।

समकोण त्रिभुजों में त्रिकोणमितीय अनुपात

मुख्य लेख : त्रिकोणमितीय फलन

एक समकोण त्रिभुज में हमेशा एक कोण 90° (π/2 रेडियन) का होता है, यहां C समकोण है। कोण A और B भिन्न-भिन्न हो सकते हैं। त्रिकोणमितीय फलन भुजा की लंबाई और त्रिभुज के आंतरिक कोणों के बीच संबंध निर्दिष्ट करते हैं।

समकोण त्रिभुजों में ज्या(sine), कोज्या(cosine) और स्पर्शज्या(tangent) अनुपातों का प्रयोग करके अज्ञात कोणों और अज्ञात भुजाओं की लंबाई को किया जा सकता है। त्रिभुज की भुजाएँ निम्नानुसार ज्ञात की जा सकती हैं:

• समकोण के सामने वाली भुजा कर्ण (hypotenuse) होती है, जो त्रिभुज की सबसे बड़ी भुजा होती है।
• लिए गए किसी कोण के सामने की भुजा लम्ब (perpendicular) होती है।
• तीसरी भुजा आधार (base) कहलाती है, जो लिए गए कोण से संपर्कित होती है।

ज्या, कोज्या और स्पर्शज्या

कोण A की ज्या, उस कोण के सामने की भुजा (लम्ब) की लंबाई और कर्ण की लंबाई का अनुपात होती है। चित्रानुसार

<math>\sin A={\frac {\text{perpendicular}}{\text{hypotenuse}}}={\frac {p}{h}}\,.</math>

कोण A की कोज्या, उस कोण की आसन्न भुजा (आधार) की लंबाई और कर्ण की लंबाई का अनुपात होती है। चित्रानुसार

<math>\cos A={\frac {\text{base}}{\text{hypotenuse}}}={\frac {b}{h}}\,.</math>

कोण A की स्पर्शज्या, उस कोण के सामने की भुजा (लम्ब) की लंबाई और उस कोण की आसन्न भुजा (आधार) की लंबाई का अनुपात होती है। चित्रानुसार

<math>\tan A={\frac {\text{perpendicular}}{\text{base}}}={\frac {p}{b}}={\frac {\sin A}{\cos A}}\,.</math>

प्रतिलोम फलन (Inverse Functions)

प्रतिलोम त्रिकोणमितीय फलनों का प्रयोग समकोण त्रिभुज में किन्हीं भी दो भुजाओं की लंबाई के द्वारा आंतरिक कोणों की गणना के लिए किया जा सकता है।

Arcsin का प्रयोग समकोण त्रिभुज में लम्ब और कर्ण की लंबाई के द्वारा आंतरिक कोण की गणना के लिए किया जा सकता है।

<math>\theta =\arcsin \left({\frac {\text{perpendicular}}{\text{hypotenuse}}}\right)</math>

Arccos का प्रयोग समकोण त्रिभुज में आधार और कर्ण की लंबाई के द्वारा आंतरिक कोण की गणना के लिए किया जा सकता है।

<math>\theta =\arccos \left({\frac {\text{base}}{\text{hypotenuse}}}\right)</math>

Arctan का प्रयोग समकोण त्रिभुज में लम्ब और आधार की लंबाई के द्वारा आंतरिक कोण की गणना के लिए किया जा सकता है।

<math>\theta =\arctan \left({\frac {\text{perpendicular}}{\text{base}}}\right)</math>

प्रारंभिक ज्यामिति और त्रिकोणमिति पाठ्यक्रमों में, sin⁻¹, cos⁻¹ आदि संकेतों का प्रयोग अक्सर arcsin, arccos आदि के स्थान पर किया जाता है। हालांकि, arcsin, arccos इत्यादि संकेत, उच्च गणित में मानक हैं, जहां त्रिकोणमितीय फलनों को आमतौर पर घातों के लिए प्रयुक्त किया जाता है, क्योंकि यह गुणात्मक प्रतिलोम और योगात्मक प्रतिलोम के बीच उलझन से बचाते हैं।

त्रिभुजों के हल

मुख्य लेख: त्रिभुजों के हल

"त्रिभुजों के हल (Solution of Triangles)" मुख्य त्रिकोणमितीय समस्या है: त्रिभुज की अज्ञात विशेषताओं (तीन कोण, तीन भुजाओं की लंबाई इत्यादि) को ढूंढना, जब इनमें कम से कम तीन विशेषताएँ दी गई हों। त्रिकोण एक समतल या गोले पर स्थित हो सकता है। यह समस्या अक्सर विभिन्न त्रिकोणमितीय अनुप्रयोगों में होती है, जैसे भूगर्भीय, खगोल विज्ञान, निर्माण, पथ प्रदर्शन इत्यादि।

त्रिभुज के क्षेत्रफल की गणना

त्रिभुज के क्षेत्रफल को, समान आधार और समान ऊंचाई के एक समांतर चतुर्भुज के क्षेत्रफल के आधे के रूप में वर्णित किया जा सकता है।

त्रिभुज के क्षेत्रफल T की गणना करना एक मूल समस्या है जो अक्सर कई अलग-अलग स्थितियों में सामने आती है। सबसे अच्छा ज्ञात और सबसे सरल सूत्र निम्न है:

<math>T={\frac {1}{2}}bh</math>

जहां b त्रिभुज के आधार की लंबाई है, और h त्रिभुज की ऊंचाई या शीर्षलंब है। "आधार" शब्द किसी भी भुजा को इंगित करता है, और "ऊंचाई" भुजा के विपरीत शीर्ष से उसी भुजा पर लंब की लंबाई को दर्शाती है। 499 CE में भारतीय गणित और भारतीय खगोल विज्ञान के शास्त्रीय युग से एक महान गणितज्ञ-खगोलविद आर्यभट्ट ने पुस्तक आर्यभट्टीय (अनुभाग 2.6) में इस विधि का उपयोग किया था।

त्रिकोणमिति के अनुप्रयोग

शीर्षलम्ब h का मान ज्ञात करने के लिए त्रिकोणमिती का प्रयोग

त्रिकोणमिति के अनुप्रयोगों से, त्रिभुज की ऊंचाई ज्ञात की जा सकती है।

दाईं ओर के चित्रानुसार, संकेतों का उपयोग करके, ऊंचाई h = a sin <math>\gamma </math> है। सूत्र <math>T={\frac {1}{2}}bh</math> में यह मान रखने पर, त्रिभुज का क्षेत्रफल निम्न प्रकार लिखा जा सकता है-

<math>T={\frac {1}{2}}ab\sin \gamma ={\frac {1}{2}}bc\sin \alpha ={\frac {1}{2}}ca\sin \beta </math>

(जहां <math>\alpha </math> शीर्ष A का आंतरिक कोण है, <math>\beta </math> शीर्ष B का आंतरिक कोण है, <math>\gamma </math> शीर्ष C का आंतरिक कोण है और c रेखा AB की लंबाई है)।

इसके अतिरिक्त, sin α = sin (π − α) = sin (β + <math>\gamma </math>), और इसी तरह अन्य दो कोणों के लिए:

<math>T={\frac {1}{2}}ab\sin(\alpha +\beta )={\frac {1}{2}}bc\sin(\beta +\gamma )={\frac {1}{2}}ca\sin(\gamma +\alpha ). </math>

<math>T={\frac {b^{2}(\sin \alpha )(\sin(\alpha +\beta ))}{2\sin \beta }}, </math>

और समान रूप से यदि भुजाएँ a व c ज्ञात हों।

<math>T={\frac {a^{2}}{2(\cot \beta +\cot \gamma )}}={\frac {a^{2}(\sin \beta )(\sin \gamma )}{2\sin(\beta +\gamma )}}, </math>

और समान रूप से यदि भुजाएँ b व c ज्ञात हों।

हेरॉन के सूत्र का उपयोग करके

त्रिभुज का आकार, भुजाओं की लंबाई से निर्धारित होता है। इसलिए, उसका क्षेत्रफल भी भुजाओं की लंबाई से ज्ञात किया जा सकता है। हेरॉन के सूत्र द्वारा:

<math>T={\sqrt {s(s-a)(s-b)(s-c)}} </math>

जहां <math>{\displaystyle s={\tfrac {a+b+c}{2}}} </math> त्रिभुज का अर्द्धपरिमाप (परिमाप का आधा) है।

हेरॉन के सूत्र को लिखने के तीन अन्य समकक्ष तरीके निम्न हैं:

<math>T={\frac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}} </math>

<math>T={\frac {1}{4}}{\sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})}} </math>

<math>T={\frac {1}{4}}{\sqrt {(a+b-c)(a-b+c)(-a+b+c)(a+b+c)}}. </math>

सदिशों का प्रयोग

एक त्रिविमीय यूक्लिडियन अंतरिक्ष में उपस्थित समांतर चतुर्भुज का क्षेत्रफल सदिशों का उपयोग करके ज्ञात किया जा सकता है। माना सदिश AB और AC, क्रमशः A से B और A से C को इंगित करते हैं। तब समांतर चतुर्भुज का क्षेत्रफल निम्न होगा-

<math>|\mathbf {AB} \times \mathbf {AC} |,</math>

जो सदिशों AB और AC के सदिश गुणन का परिमाण है। त्रिभुज ABC का क्षेत्रफल इसका आधा होता है,

<math>{\frac {1}{2}}|\mathbf {AB} \times \mathbf {AC} |.</math>

त्रिभुज ABC का क्षेत्रफल अदिश गुणन के संदर्भ में भी निम्नानुसार व्यक्त किया जा सकता है:

<math>{\frac {1}{2}}{\sqrt {(\mathbf {AB} \cdot \mathbf {AB} )(\mathbf {AC} \cdot \mathbf {AC} )-(\mathbf {AB} \cdot \mathbf {AC} )^{2}}}={\frac {1}{2}}{\sqrt {|\mathbf {AB} |^{2}|\mathbf {AC} |^{2}-(\mathbf {AB} \cdot \mathbf {AC} )^{2}}}.\,</math>

द्विविमीय यूक्लिडियन अन्तरिक्ष में, कार्तीय तल में एक मुक्त सदिश के रूप में सदिश AB को (x₁,y₁) और सदिश AC को (x₂,y₂) व्यक्त करने पर, इसे निम्न प्रकार लिखा जा सकता है:

<math>{\frac {1}{2}}\,|x_{1}y_{2}-x_{2}y_{1}|.\,</math>

== इन्हें भी देखें ==(त्रिभुजों के तीन कोण होते है।1.अधिक कोण त्रिभुज 2.समकोण त्रिभुज 3.नयुन त्रिभुजों

• [पाइथागोरस प्रमेय]]
• त्रिकोणीय सर्वेक्षण
• त्रिभुजों के हल