आयलर समीकरण
चिरसम्मत यांत्रिकी में, आयलर के घूर्णी समीकरण घूर्णी निर्देश तन्त्र की सहायता से दृढ़ पिण्डों की घूर्णन गति का वर्णन करते हैं। इसमें जो घूर्णी फ्रेम लिया जाता है उसका अक्ष उस पिण्ड से जुड़ा हुआ (फिक्ड) तथा पिण्ड के मुख्य जड़त्व अक्षों के समान्तर होता है। आयलर समीकरण, सदिश अर्धरैखिक प्रथम ऑर्डर वाले साधारण अवकल समीकरण होते हैं। आयलर समीकरणों का सामान्य रूप निम्नलिखित है-
- <math>
\mathbf{I} \cdot \dot{\boldsymbol\omega} + \boldsymbol\omega \times \left( \mathbf{I} \cdot \boldsymbol\omega \right) = \mathbf{M}. </math> जहाँ M लगाये गये बलाघूर्ण हैं, I जड़तवाघूर्ण मैट्रिक्स (inertia matrix) है, ω मुख्य अक्षों के सापेक्ष कोणीय वेग है।
3D मुख्य लम्बकोणिक अक्षों (orthogonal coordinates) में उपरोक्त समीकरणों का निम्नलिखित रूप हो जाता है-
- <math>
\begin{align} I_1\dot{\omega}_{1}+(I_3-I_2)\omega_2\omega_3 &= M_{1}\\ I_2\dot{\omega}_{2}+(I_1-I_3)\omega_3\omega_1 &= M_{2}\\ I_3\dot{\omega}_{3}+(I_2-I_1)\omega_1\omega_2 &= M_{3} \end{align} </math>
जहाँ Mk आरोपित बलाघूर्ण M के घटक हैं, Ik मुख्य जड़त्व आघूर्ण अक्ष I के घटक हैं और ωk कोणीय वेग ω के घटक मुख्य अक्षों की दिशा हैं।
अभिप्रेरण और व्युत्पत्ति
आयलर के द्वितीय नियम से आरम्भ करने पर, एक जड़त्वीय निर्देश तन्त्र ("in" अधोलिखित) में, कोणीय संवेग L का समय के सापेक्ष अवकलन आरोपित बलाघूर्ण के बराबर होता है
- <math>
\frac{d\mathbf{L}_{\text{in}}}{dt} \ \stackrel{\mathrm{def}}{=}\ \frac{d}{dt} \left(\mathbf{I}_{\text{in}} \cdot \boldsymbol\omega \right) = \mathbf{M}_{\text{in}} </math>
जहाँ Iin जड़त्वीय निर्देश तन्त्र में परिकलित जड़त्वाघूर्ण प्रदिश है। यद्यपि यह नियम सार्वभौमिक सत्य है, यह समान्य घूर्णी दृढ़ पिण्ड की गति के लिए हल करने में हमेशा सहायक नहीं है। चूँकि Iin और ω दोनों गति के दौरान परिवर्तित हो सकते हैं।
अतः हम निर्देश तन्त्र को इस तरह परिवर्तित करते हैं कि वह घूर्णी पिण्ड के साथ स्थिर रहे और इस तरह से चयन करते हैं कि इसकी अक्ष जड़त्वाघूर्ण प्रदिश की दिशा में स्थित हों। इस निर्देश तन्त्र में कम से कम जड़त्वाघूर्ण प्रदिश तो नियत (और विकर्ण) है, जो गणना को सुगम बनाता है। जैसा की जड़त्वाघूर्ण में समझाया गया है, कोणीय संवेग
- <math>
\mathbf{L} \ \stackrel{\mathrm{def}}{=}\ L_{1}\mathbf{e}_{1} + L_{2}\mathbf{e}_{2} + L_{3}\mathbf{e}_{3} = I_{1}\omega_{1}\mathbf{e}_{1} + I_{2}\omega_{2}\mathbf{e}_{2} + I_{3}\omega_{3}\mathbf{e}_{3} </math>
जहाँ Mk, Ik और ωk उपर वर्णित किए गये अनुसार हैं।
घूर्णी निर्देश तन्त्र में, समय अवकलज को
- <math>
\left(\frac{d\mathbf{L}}{dt}\right)_\mathrm{rot}+ \boldsymbol\omega\times\mathbf{L}=\mathbf{M} </math> से प्रतिस्थापित करना चाहिये।
जहाँ अधोलिखित "rot" घूर्णी निर्देश तन्त्र को निरुपित कर रहा है। जड़त्वीय और घूर्णी निर्देश तन्त्रों में बलाघूर्ण से सम्बंधित व्यंजक निम्न है :
- <math>
\mathbf{M}_{\text{in}} = \mathbf{Q}\mathbf{M}, </math>
जहाँ Q घूर्णी प्रदिश है, जो किसी कोणीय वेग सदिश v से सम्बंधित लंब कोणीय प्रदिश है
- <math>\boldsymbol\omega \times \boldsymbol{v} = \dot{\mathbf{Q}} \mathbf{Q}^{-1}\boldsymbol{v}</math>
बलाघूर्ण स्वतंत्र हल
अनुप्रयोग
बिलियर्ड की गेंद को धक्का
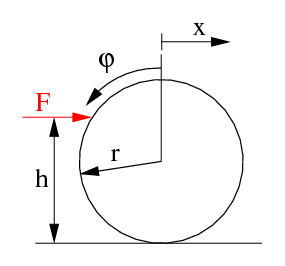
सामने के चित्र में r त्रिज्या, m द्रव्यमान एवं I जड़त्वाघूर्ण वाली एक बिलियर्ड की गेंद को टेबल के समान्तर इस प्रकार मारना है कि गेंद टेबल पर बिना सरके हुए आगे बढ़े (लुढ़के)। हम इसमें यह जानना चाहते हैं कि गेंद के आधार से किस ऊँचाई पर बल F लगाया जाय ताकि कोई घर्षण बल न होने के वावजूद गेंद बिना फिसले, लुढ़कते हुए आगे बढ़ जाय।
क्षैतिज दिशा में लगाये गये बल F का बलाघूर्ण M = - (h-r) F गेंद में घूर्णी त्वरण पैदा करता है-
- <math>M=-(h-r)F=I\ddot\varphi</math>
यहाँ बलाघूर्ण ऋणात्मक लिया गया है क्योंकि यह घूर्णन कोण φ के विपरीत है (चित्र देखें)। इस समीकरण के अलावा, गेंद पर लगाये गये बल F के कारण उसके द्रव्यमान केन्द्र में त्वरण उत्पन्न होत है। अतः
- <math>F=m\ddot x\,.</math>
ध्यान दीजिये कि त्वरण <math>\ddot x</math> , टेबल के समान्तर तथा बल की दिशा में है। बिना-सरके लुढ़कने के लिये आवश्यक है कि-
- <math>\ddot x=-r\ddot\varphi</math>
इस प्रकार उपरोक्त सभी समीकरण मिलकर गेंद की गति का तीन चरों h, φ, तथा x में वर्णन करते हैं। इन समीकरणों को मिलाकर हल करते हुए हमें निम्नलिखित जानकारी मिलती है-
- <math>-(h-r)F=I\ddot\varphi=-\frac{I}{r}\ddot x=-\frac{I}{mr}F
\quad\rightarrow\quad h=r+\frac{I}{mr} \,.</math>
किसी ठोस, समांग गोले का जड़त्वाघूर्ण <math>I=\tfrac{2}{5}mr^2</math> होता है। यह मान रखने पर-
- <math>h=\frac{7}{5}r</math>
नत समतल पर बेलन की गति
r त्रिज्या, m द्रव्यमान तथा I जड़त्वाघूर्ण वाला एक पहिया (या, बेलन) α कोण पर झुके हुए समतल पर गुरुत्वीय त्वरण g के प्रभ से लोटनी गति (रोल्लिंग) कर रहा है। (सामने का चित्र देखें)। चूँकि यह पहिया स्थानान्तरित भी हो रहा है, इसके द्रव्यमान का रैखिक त्वरण भी हो रहा है। इस समस्या में हम यह मान रहे हैं कि पहिये की गति बिना सरके (बिना स्लिप के) हो रही है। अतः नत-समतल और पहिये के बीच (सम्पर्क बिन्दु पर) एक घर्षण बल R उत्पन्न होता है जो पहिये को घुमाता है, क्योंकि इस बल के कारण एक बलाघूर्ण M = -r R लगता है। यह बलाघूर्ण ऋणात्मक लिया गया है क्योंकि यह घूर्णन कोण φ के विपरीत है। अतः पहिये की घूर्णन गति का समीकरण निम्नलिखित है-
- <math>-r R=I\ddot\varphi\,.</math>
अब पहिये के द्रव्यमान केन्द्र के विस्थापन पर विचार करते हैं। पहिये के द्रव्यमान mg का नत-समतल की दिशा में अवयव (कम्पोनेन्ट) F का मान F=mgsin(α) है। यह बल घर्षण बल के उल्टी दिशा में कार्य कर रहा है। अतः न्यूटन की गति के द्वितीय नियम के अनुसार-
- <math>F-R=m\ddot x
\quad\rightarrow\quad R=mg\sin(\alpha)-m\ddot x \,,</math>
जहाँ <math>\ddot x</math> पहिये का नत-समतल के समान्तर (नीचे की ओर) त्वरण है। इसके अलावा, यदि लोटन गति बिना फिसले हुए हो रही है तो <math>\ddot x=-r\ddot\varphi</math>। इस प्रकार हमने तीन अज्ञात राशियों R, φ तथा x को समेटे हुए गति के समीकरण प्राप्त कर लिये। इन समीकरणों को हल करने पर हमे यह प्राप्त होता है-
- <math>\begin{align}
\ddot\varphi=&-\frac{mr^2}{I+mr^2}\frac{g}{r}\sin(\alpha)=-\frac{r}{I+mr^2}F \\ R=&\frac{I}{I+mr^2}mg\sin(\alpha)=\frac{I}{I+mr^2}F \\ \ddot x=&\frac{mr^2}{I+mr^2}g\sin(\alpha)=\frac{r^2}{I+mr^2}F \,.\end{align}</math>
इससे यह देखा जा सकता है कि किसी दिये हुए नत-कोण α के लिये, अधिकतम त्वरण तब होता है जब पहिये का द्रव्यमान अधिक-से-अधिक उसके अक्ष के निकट हो। (अर्थात जड़त्वाघूर्ण न्यूनतम हो)।
ध्यान दीजिये कि इसी नत-समतल पर, यदि घर्षण शून्य हो तो, उस पर सरक रहे किसी पिण्ड का त्वरण <math>\ddot x=g\sin(\alpha)</math> (नत से समान्तर, नीचे की तरफ) होगा, जो पहिये के त्वरण से अधिक है। इसका कारण यह है कि पहिये की स्थितिज ऊर्जा दो प्रकार की गतिज ऊर्जा में बदल रही है- घूर्णन की गतिज ऊर्जा तथा द्रव्यमान केन्द्र के स्थानान्तरण की गतिज ऊर्जा ; जबकि सरकते हुए पिण्ड में केवल एक ही गतिज ऊर्जा होती है- द्रव्यमान केन्द्र के स्थानान्तरण की गतिज ऊर्जा (सरकते हुए पिण्ड के लिये, घूर्णन ऊर्जा शून्य होती है।)
ये भी देखें
सन्दर्भ
- C. A. Truesdell, III (1991) A First Course in Rational Continuum Mechanics. Vol. 1: General Concepts, 2nd ed., Academic Press. ISBN 0-12-701300-8. Sects. I.8-10.
- C. A. Truesdell, III and R. A. Toupin (1960) The Classical Field Theories, in S. Flügge (ed.) Encyclopedia of Physics. Vol. III/1: Principles of Classical Mechanics and Field Theory, Springer-Verlag. Sects. 166-168, 196-197, and 294.
- Landau L.D. and Lifshitz E.M. (1976) Mechanics, 3rd. ed., Pergamon Press. ISBN 0-08-021022-8 (hardcover) and ISBN 0-08-029141-4 (softcover).
- Goldstein H. (1980) Classical Mechanics, 2nd ed., Addison-Wesley. ISBN 0-201-02918-9
- Symon KR. (1971) Mechanics, 3rd. ed., Addison-Wesley. ISBN 0-201-07392-7