घूर्णाक्षदर्शी

घूर्णदर्शी और उसके भाग

घूर्णाक्षदर्शी या घूर्णदर्शी (जाइरोस्कोप/Gyroscope) एक युक्ति है जो किसी वस्तु की कोणीय स्थिति (झुकाव) को मापने के काम आता है। इसकी क्रियाविधि कोणीय संवेग के संरक्षण के सिद्धान्त पर आधारित है। घूर्णदर्शी का प्रयोग जहाँ चुम्बकीय सूई काम नहीं करती वहाँ भी नेविगेशन में होती है (जैसे हबल अंतरिक्ष दूरदर्शी में)। ये चुम्बकीय सूई की अपेक्षा अधिक सूक्ष्ममापी (प्रेसाइज) भी होते हैं जिसके कारण अन्तरमहाद्वीपीय बैलिस्टिक प्रक्षेपास्त्रों एवं रेडियो-नियंत्रित हेलिकॉप्टरों आदि में इसका उपयोग किया जाता है।

यांत्रिक घूर्णदर्शी की संरचना

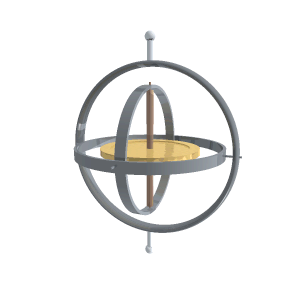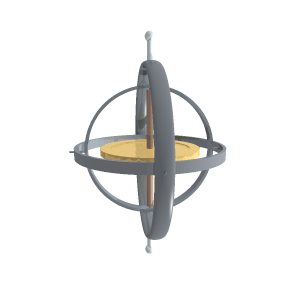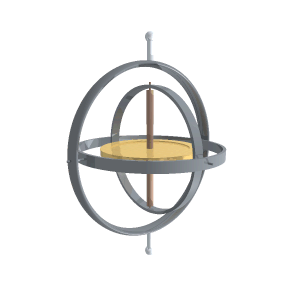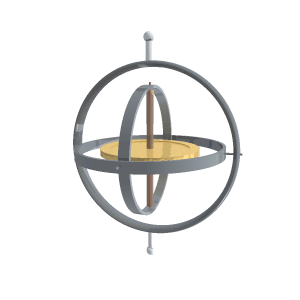
घूर्णदर्शी यांत्रिक हो सकता है और एलेक्ट्रानिक भी। यांत्रिक घूर्णदर्शी एक संतुलित चक्र या पहिया होता हैं, जो इस प्रकार आधार वलयों (supporting rings) में स्थापित रहता है कि इसकी तीन स्वातंत्र्य संख्याएँ (degrees of freedom) होती हैं। इस पहिए को घूर्णक या रोटर (rotor) भी कहते हैं। यह चक्र एक अक्ष या धुरी के चारों और परिभ्रमण कर सकने के लिये स्वतंत्र होता है। इस अक्ष को भ्रमि अक्ष (spinning axis) कहते हैं। यह अक्ष या धुरी एक आधार वलय में उसके क्षैतिज व्यास पर स्थित रहती है और यह वलय स्वंय भी एक अन्य बाह्य वलय में एक क्षैतिज अक्ष के चारों ओर परिभ्रमण कर सकता है। यह अक्ष भ्रमि अक्ष के समकोणिक होता है। बाह्य वलय भी एक ऊर्ध्वाधर अक्ष के चारों ओर घूम सकता है। इस प्रकार इस चक्र या घूर्णक की धुरी किसी भी इच्छित दिशा में इंगित करती हुई रखी जा सकती है। भ्रमि करते समय यह चक्र दो मूल घूर्णदर्शी गुणों का प्रदर्शन करता है : (1) अवस्थितत्व (inertia) (2) पुरस्सरण (precession)। घूर्णदर्शी को भली भाँति समझने के लिये इन गुणों के लक्षणों को भी समझ लेना नितांत आवश्यक है।

घूर्णाक्षदर्शी का पुरस्सरण (Precession)

न्यूटन के प्रथम गतिनियम के अनुसार कोई भी पिंड जिस अवस्था में रहता है उसी में बना रहना चाहता है और उस अवस्था में किसी प्रकार के परिवर्तन का विरोध करने की प्रवृत्ति प्रदर्शित करता है। इस प्रवृत्ति को जड़त्व (inertia) कहते हैं। अपनी धुरी पर भ्रमण करता हुआ रोटर अपने प्रारंभिक तल में ही परिभ्रमण करना चाहता है और कोई बलघूर्ण (torque) स्थापित करने पर उसका विरोध करता है।

घूर्णदर्शी के रोटर की दूसरी विशेषता है पुरस्सरण। परिभ्रमण करते हुए किसी पिंड के कोणीय संवेग में परिवर्तन करने के लिये एक बलाघूर्ण आवश्यक होता है। यदि बलाधूर्ण और कोणीय संवेग के अक्ष परस्पर संपाती (coincident) होते हैं, तो उस पिंड में एक कोणीय त्वरण उत्पन्न हो जाता है, किंतु उस पिंड के परिभ्रमण का तल अपरिवर्तित रहता है। इसके विपरीत यदि उक्त दोनों अक्ष परस्पर सम-कोणिक होते हैं, तो पिंड के कोणीय वेग में कोई अंतर नहीं आता, किंतु परिभ्रमण का तल स्वयं ही घूमने लगता है। इस प्रकार की गति को पुरस्सरण कहते हैं।

घूर्णदर्शी का सिद्धान्त

तीनों अक्षों में घूमने के लिये स्वतंत्र घूर्णदर्शी : बाहरी वलय का झुकाव चाहे कुछ भी हो, रोटर की स्पिन-अक्ष की दिशा नहीं बदलेगी

घूर्णक्षस्थापी की क्रियाएँ सभी परिभ्रमणशील या घूर्णशील पिंडों में दृष्टिगोचर होती है, किंतु अधिक कोणीय संवेग (momentum) वाले पिंडों में ये क्रियाएँ अधिक स्पष्ट होती हैं। कोणीय संवेग के कारण ही घूर्णाक्षस्थापी में दृढ़ता तथा जड़त्व के गुणों का समावेश होता है।

किसी पिंड पर जब कोई बलयुग्म कार्य करता है, तब उस पिंड में बलयुग्म (couple) के अक्ष के चारों ओर एक कोणीय संवेग उत्पन्न हो जाता है, जिसके कारण पिण्ड में उस अक्ष के चारों और भ्रमि करने की प्रवृत्ति उत्पन्न हो जाती है। जितने समय तक वह बलयुग्म कार्य करता रहेगा उतने समय तक उस पिंड का कोणीय वेग बढ़ता ही जाएगा।

निम्नलिखित समीकरण घूर्णाक्षदर्शी के गुण को अभिव्यक्त करता है-

<math>\vec\tau={{d \vec L}\over {dt}}={{d(I\vec \omega)} \over {dt}}= I\vec \alpha</math>

जहाँ सदिश <math>\vec\tau</math> तथा <math>\vec L</math> क्रमशः घूर्णाक्षदर्शी पर आरोपित बलाघूर्ण तथा कोणीय संवेग हैं। अदिश I इसका जड़त्वाघूर्ण है, सदिश <math>\vec\omega</math> इसका कोणीय वेग है, और सदिश <math>\vec\alpha</math> कोणीय त्वरण है।

इस समीकरण से स्पष्ट है कि यदि बलाघूर्ण <math>\vec\tau</math> को घूर्णन-अक्ष के लम्बवत लगाया जाय (अर्थात <math>\vec{L}</math> के लम्बवत) तो इसके कारण <math>\vec\tau</math> तथा <math>\vec L</math> दोनों के लम्बवत विस्थापन उत्पन्न होगा। इस गति को पुरस्सरण (précession) कहते हैं। पुरस्सरण का कोणीय वेग Ωसाँचा:ind का व्यंजक निम्नलिखित होगा-

<math>\vec\tau={\vec \Omega}_P \wedge \vec L</math>

मान लिया, एक भारी चक्र (या पहिया) एक क्षैतिज धुरी क-ख पर नर्तन (भ्रमि) कर रहा है। धुरी के दोनों सिरों पर दो बल F और F इस प्रकार कार्य कर रहे हैं कि उनसे एक बलयुग्म का निर्माण होता है। इससे उत्पन्न होने वाला बलघूर्ण G = F.l, जहाँ l अक्ष क-ख की लंबाई है। इसके परिणामस्वरूप यह संपूर्ण प्रणाली एक अन्य लांबिक अक्ष के चारों ओर पुरस्सृत (precess) होने लगेगी। यदि चक्र के परिभ्रमण का वेग w तथा पुरस्सरण की दर w¢ हो तो G = I . w . w¢, जहाँ I उस चक्र का नर्तन अक्ष के चारों ओर जड़त्वाघूर्ण (moment of Inertia), है। अत: यदि चक्र का कोणीय संवेग I w काफी अधिक होगा तो w ¢ का मान बहुत कम होगा।

इससे स्पष्ट है कि बहुत अधिक जड़त्वाघूर्णवाला चक्र (जैसे गतिपालक चक्र या फ्लाई-ह्वील) यदि किसी अक्ष के चारों ओर बहुत तेजी से परिभ्रमण कर रहा हो, तो उस पर किसी बाहरी अल्पकालिक बलघूर्ण, G, का प्रभाव अत्यंत क्षीण पड़ेगा, अर्थात् विघ्नकारी बाह्य बलों से वह व्यवहारत: अप्रभावित रहेगा। कोणीय संवेग अधिक हो इस हेतु काफी अधिक व्यासवाला गतिपालक चक्र (फ्लाई-ह्वील) घूर्णाक्षस्थापी में प्रयुक्त किया जाता है। इसके अतिरिक्त भ्रमि वेग w बढ़ाकर भी घूर्णक्षस्थापी के कोणीय संवेग में बहुत अधिक सीमा तक वृद्धि की जा सकती है। इससे घूर्णक्षस्थापी पर किसी अल्पायु बाह्य बलयुग्म का प्रभाव नहीं पड़ सकता।

उपर्युक्त गुण के कारण घूर्णाक्षस्थापी का प्रयोग पृथ्वी के परिभ्रमण का दिग्दर्शन करने के हेतु किया जा सकता है। पृथ्वी अपनी धुरी पर पश्चिम से पूर्व की दिशा में परिभ्रमण करती है। इसका एक परिभ्रमण 24 घंटों में पूरा होता है। यदि किसी घूर्णाक्षस्थापी को पृथ्वी तल के किसी स्थान पर इस प्रकार रखा जाय कि उसका भूमि अक्ष पूर्व पश्चिम दिशा में क्षैतिज रहे, तो पृथ्वी के परिभ्रमण के साथ साथ उसका संपूर्ण ढांचा (frame work) भी पृथ्वी के केंद्र की परिक्रमा करेगा, क्योंकि प्रत्येक समय उस ढाँचे का तल पृथ्वी-तल के लंबवत् (ऊर्घ्वाधर) रहेगा। किंतु अपने जड़त्व तथा अत्यधिक कोणीय संवेग के कारण भूमि अक्ष अपनी प्रारंभिक दिशा के ही समांतर रहेगा। इसलिये पृथ्वी के परिभ्रमण के कारण भ्रमिअक्ष, जो प्रारंभ में पृथ्वीतल के समांतर था, प्रति क्षण कुछ कोण बनाता हुआ दिखलाई पड़ेगा। इस प्रकार घूणक्षिस्थापी का भ्रमिअक्ष अपने समकोणिक एकक्षैतिज अक्ष के चारों ओर पुरस्सरण करता हुआ प्रतीत होगा।

इतिहास

घूर्णदर्शी का सर्वप्रथम उपयोगी रूप जर्मन गणिज्ञ जोहैन बोएनबर्गर (Johann Bohenberge, 1765-1831) ने प्रस्तुत किया था। सन् 1817 ई॰ में उसने इसका अपने ज्योतिष अनुंसधान के क्रम में किए गए प्रयोगों में अत्यंत सफलतापूर्वक व्यवहार किया और इसके बाद इसका विवरण विज्ञानजगत् के समक्ष प्रस्तुत किया। बाद में लीओं फूकों (Leon Founcault) ने पृथ्वी के परिभ्रमण को प्रमाणित करने के हेतु इसका प्रयोग किया। यद्यपि घूर्णदर्शी पर छोटे-मोटे अथवा अल्पकालिक बलों अथवा बलघूर्णो का कोई दृश्यमान प्रभाव नहीं पड़ता, फिर भी भ्रमिधुरी और बॉलबेयरिंगों के बीच घर्षण इत्यादि के कारण यह उतना सटीक परिणाम नहीं दे पाता जितना सिद्धांतत: इसे देना चाहिए। इसके लिये आवश्यक संशोधन कर देने से एतज्जनित त्रुटियों का परिहार किया जा सकता है।

घूर्णदर्शी के व्यावहारिक उपयोग

वायुयान, मिसाइल, आदि में प्रयुक्त आधुनिक घूर्णाक्षदर्शी जिसका निर्माण Sperry Co. Corporation ने किया है।

घूर्णदर्शी के कुछ महत्वपूर्ण व्यावहारिक उपयोग निम्नलिखित हैं :

• 1. घूर्णक्षस्थिरक (Gyro-stabilizer) के रूप में - बाह्य-बलघूर्ण के द्वारा अप्रभावित रहने के घूर्णाक्षस्थापी के गुण का उपयोग सागर के वक्ष पर यात्रा करनेवाले जलयानों को उत्ताल तरंगों के धक्कों से डगमगाने, या उलटने, से बचाने के लिये किया जाता है। इससे सागरीय यात्रा अधिक निरापद एवं कष्टरहित बनाई जा सकी है। जलयानों के डेकों के नीचे यान की केंद्ररेखा पर एक घूर्णाक्षस्थापी लगा दिया जाता है जिसका चक्र, या घूर्णक, विशेष प्रकार के दृढ़ इस्पात का बना होता है। इस घूर्णदर्शी का भ्रमिअक्ष ऊर्ध्वाधर होता है। जब तंरगों के झोंकां से जलयान दाहिने बाएँ डगमगाता है तब भी इसका भ्रमिअक्ष पूर्ववत् ऊर्ध्वाधर बना रहता है। इस कारण वह तंरगों के विरुद्ध एक प्रतिकारी बलघूर्ण का सृजन कर उन्हें संतुलित करता है और इस प्रकर जलयान को सीधा रखने का प्रयत्न करता है। इससे जलयानों का झुकाव किसी भी ओर ऊर्ध्वाधर से चार या पाँच अंशों से अधिक नहीं होने पाता और उसके यात्रियों को तज्जनित कष्ट या असुविधा की अनुभूति नहीं होती।

• 2. घूर्णदर्शी का सर्वाधिक महत्वपूर्ण उपयोग वायुयानों के परिचालन में किया जाता है। उनमें इसका उपयोग दो प्रकार से होता है :

(क) दिशासूचक घूर्णदर्शी के रूप में, और

(ख) कृत्रिम क्षितिज के रूप में।

वायुयानों के दिशानियंत्रण के लिये घूर्णदर्शी अनिवार्य उपकरण बन गया है। दिशासूचक घूर्णदर्शी वायुयान के यंत्रपटल पर चालक के ठीक सामने लगा रहता है। अपनी प्रारंभिक स्थिति में इसकी भ्रमिधुरी पृथ्वी तल के ठीक समांतर रहती है। इसके चक्र के ठीक सामने एक छिद्र होता है, जिसमें से होकर आनेवाली वायु का प्रबल झोंका चक्र को बड़ी तेजी से घुमाता रहता है। उड़ते समय वायुयान को जब घुमाया जाता है तब घूर्णदर्शी की भ्रमिधुरी अपनी प्रारंभिक दिशा में रहती है। इसलिये वायुयान का घुमाव ठीक ठीक ज्ञात हो जाता है। सामान्यता वायुयानों में चुम्बकीय दिक्सूचक द्वारा दिशा का ज्ञान किया जाता है, किंतु वायुयान घुमाते समय, अथवा वायु के झोंकों के करण, उसकी सूई अनियमित रूप से इधर उधर घूमने लगती है और तत्काल ठीक ठीक दिशा ज्ञात नहीं हो पाती। घूर्णदर्शी इन सबसे सर्वथा अप्रभावित रहता है। इसलिये यह एक प्रकार से चुंबकीय दिक्सूचक के पूरक की भाँति कार्य करता है और चालक को उसके गंतव्य की ठीक ठीक दिशा ज्ञात कराने में सहायक होता है।

एक दूसरा घूर्णदर्शी चालक को यही ठीक ठीक बतलाता है कि वह कितने ऊँचे या नीचे जा रहा है। धरती से बहुत ऊँचाई पर उड़नेवाले वायुयान के चालक को यह पता लगाना कठिन होता है कि उसका यान ऊपर या नीचे की ओर किस दिशा में जा रहा है। इसलिये उसे इस घूर्णदर्शी की सहायता लेनी पड़ती है। इसके भ्रमिअक्ष की प्रारंभिक दिशा ऊर्ध्वाधर होती है। जब वायुयान ऊपर चढ़ता या नीचे उतरता है, तब वायुयान तल के ऊर्ध्वाधर से इस अक्ष के झुकाव द्वारा वायुयान की दिशा का ठीक ठीक ज्ञान हो जाता है। इस घूर्णदर्शी का कृत्रिम क्षितिज कहते हैं, क्योंकि इससे वही सहायता ली जाती है जो पृथ्वी पर क्षितिज से मिलती है। के अनुसार कोई भी पिंड जिस अवस्था में रहता है उसी में बना रहना चाहता है और उस अवस्था में किसी प्रकार के परिवर्तन का विरोध करने की प्रवृत्ति प्रदर्शित करता है। इस प्रवृत्ति को जड़त्व (inertia) कहते हैं। अपनी धुरी पर भ्रमण करता हुआ रोटर अपने प्रारंभिक तल में ही परिभ्रमण करना चाहता है और कोई बलघूर्ण (torque) स्थापित करने पर उसका विरोध करता है।

विभिन्न रूप

• Gyrostat

• MEMS

• HRG

• VSG (vibrating structure gyroscope) या CVG (Coriolis vibratory gyroscope)

• DTG (dynamically tuned gyroscope)

• Ring laser

• Fiber optic gyroscope

• London moment

इन्हें भी देखें

• जाइरेटर (Gyrator)
• जड़त्वाघूर्ण
• कोणीय संवेग
• पुरस्सरण

बाहरी कड़ियाँ

• U.S. Dynamics Long Life Gyroscopes
• Technical White Papers on Gyroscopes
• Description of the Systron Donner Inertial MEMS gyroscope
• The Precession and Nutation of a Gyroscope
• Everything you needed to know about gyroscopes
• Project in which gyroscopes are used to drive a robotic arm
• Examples of gyroscopes
• An explanation of gyroscopes

शोधपत्र

• Theory and Design of Micromechanical Vibratory Gyroscopes Vladislav Apostolyuk

व्याख्यान

• The Royal Institution’s 1974–75 Christmas Lecture Professor Eric Laithwaite