त्रिकोणमिति

किसी दूरस्थ और सीधे मापन में कठिन सर्वेक्षण के लिए समरूप त्रिभुज के उपयोग का उदाहरण (1667)

त्रिकोणमिति गणित की वह शाखा है जिसमें त्रिभुज और त्रिभुजों से बनने वाले बहुभुजों का अध्ययन होता है। त्रिकोणमिति का शब्दिक अर्थ है 'त्रिभुज का मापन'। अर्थात् त्रिभुज की भुजाओं का मापन अतः त्रिकोणमिति गणित का वह भाग है जिसमें त्रिभुज कि भुजाओं के मापन का अध्ययन किया जाता है। त्रिकोणमिति में सबसे अधिक महत्वपूर्ण है समकोण त्रिभुज का अध्ययन। त्रिभुजों और बहुभुजों की भुजाओं की लम्बाई और दो भुजाओं के बीच के कोणों का अध्ययन करने का मुख्य आधार यह है कि समकोण त्रिभुज की किन्ही दो भुजाओं (आधार, लम्ब व कर्ण) का अनुपात उस त्रिभुज के कोणों के मान पर निर्भर करता है। त्रिकोणमिति का ज्यामिति की प्रसिद्ध बौधायन प्रमेय (पाइथागोरस प्रमेय ) से गहरा सम्बन्ध है।

त्रिकोणमितीय अनुपात

त्रिभुज ABC

इकाई त्रिज्या वाले एक वृत्त की सहायता से किसी कोण θ के सभी त्रिकोणमितीय फलन ज्यामितीय रूप से दर्शाये जा सकते हैं।

ज्या sine

कोज्या (कोज) cosine

स्पर्शज्या (स्पर) tan

व्युज्या (व्युज) cosec

व्युकोज्या (व्युक) sec

व्युस्पर्शज्या (व्युस) cot

एक समकोण त्रिभुज की तीनों भुजाओं (कर्ण, लम्ब व आधार) की लम्बाई के आपस में अनुपातों को त्रिकोणमितीय अनुपात कहा जाता है। तीन प्रमुख त्रिकोणमितीय अनुपात हैं:

ज्या (स) = लम्ब/कर्ण

कोज (स)= आधार/कर्ण

स्पर (स)= लम्ब/आधार

बाकी तीन अनुपात ऊपर के अनुपातों का व्युत्क्रम होते हैं:

व्युज (स) = कर्ण/लम्ब

व्युक (स)= कर्ण/आधार

व्युस (स)= आधार/लम्ब

कोण स आधार और कर्ण के बीच के कोण का मान है। त्रिकोणमिति की लगभग सभी गणनाओं में त्रिकोणमितीय अनुपातों का प्रयोग किया जाता है।

स्पर (स) = ज्या (स) / कोज (स)

व्युस (स) = कोज (स) / ज्या (स)

दूसरा तरीका : त्रिकोणमित्तीय फलनों की परिभाषा कोण के 'सामने की भुजा', 'संलग्न भुजा' एवं कर्ण के अनुपातों के रूप में याद करने से कभी 'लम्ब' या 'आधार' का भ्रम नहीं रहता। नीचे opp = सामने की भुजा ; adj = संलग्न भुजा तथा hyp = कर्ण

<math> \sin A = {\mbox{opp} \over \mbox{hyp}} = {a \over c}

\qquad \cos A = {\mbox{adj} \over \mbox{hyp}} = {b \over c}
\qquad \tan A = {\mbox{opp} \over \mbox{adj}} = {a \over b}

</math>

त्रिकोणमितीय अनुपात और बौधायन प्रमेय

बौधायन प्रमेय के अनुसार : कर्ण^२ = लम्ब^२ + आधार^२

इस प्रकार किसी भी कोण स के लिये : ज्या^२(स) + कोज^२(स) = १

बौधायन प्रमेय से यह भी स्पष्ट है कि किसी भी कोण के लिये ज्या और कोज्या का धनात्मक मान ० और १ के बीच ही हो सकता है।

कुछ कोणों का त्रिकोणमितीय मान

टिप्पणी : भारत के महान गणितज्ञ आर्यभट्ट ने चौथी शताब्दी में शून्य से ९० अंश के बीच चौबीस कोणों के ज्या के मानों की सारणी प्रस्तुत की थी।

निम्नलिखित तालिका कुछ प्रमुख कोणों का त्रिकोणमितीय मान दर्शाती है:

स	ज्या	कोज्या	स्पर्शज्या	कोस्पर्शज्या	व्युकोज्या	व्युज्या
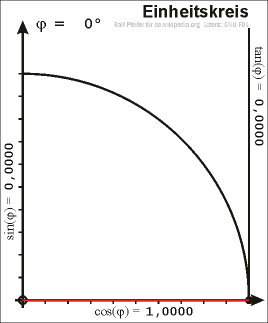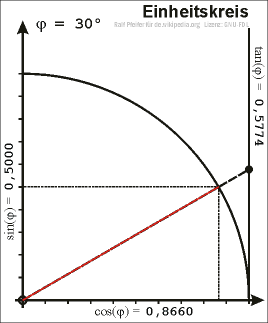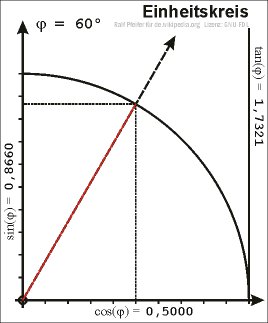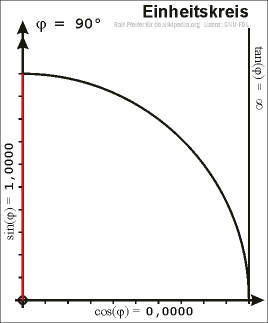
०°	<math>0</math>	<math>1</math>	<math>0</math>	<math>\infty</math>	<math>1</math>	<math>\infty</math>
३०°	<math>1/2</math>	<math>\sqrt{3}/2</math>	<math>1/\sqrt{3}</math>	<math>\sqrt{3}</math>	<math>2/\sqrt{3}</math>	<math>2</math>
४५°	<math>1/\sqrt{2}</math>	<math>1/\sqrt{2}</math>	<math>1</math>	<math>1</math>	<math>\sqrt{2}</math>	<math>\sqrt{2}</math>
६०°	<math>\sqrt{3}/2</math>	<math>1/2</math>	<math>\sqrt{3}</math>	<math>1/\sqrt{3}</math>	<math>2</math>	<math>2/\sqrt{3}</math>
९०°	<math>1</math>	<math>0</math>	<math>\infty</math>	<math>0</math>	<math>\infty</math>	<math>1</math>

प्रमुख त्रिकोणमितीय सूत्र

<math>\sin(-\alpha) = - \sin(\alpha)</math> <math>\cos(-\alpha) = \cos(\alpha)</math> <math>\tan\alpha = \frac{\sin\alpha}{\cos\alpha}</math> <math>\tan(-\alpha) = - \tan(\alpha)</math> <math>\sin^2 \alpha + \cos^2 \alpha = 1</math> <math> \cot\alpha = \frac{1}{\tan\alpha}</math> <math> \sec\alpha = \frac{1}{\cos\alpha}</math> <math> \csc\alpha = \frac{1}{\sin\alpha}</math>

<math> \sin \alpha = \sqrt{1 - \cos^2 \alpha}</math> <math> \sin \alpha = \frac{\tan \alpha}{ \sqrt{1 + \tan^2 \alpha} } </math> <math> \cos \alpha = \sqrt{1 - \sin^2 \alpha}</math> <math> \cos \alpha = \frac{1}{\sqrt{1 + \tan^2 \alpha} } </math> <math> \tan \alpha = \frac{\sqrt{1 - \cos^2 \alpha} }{\cos \alpha} </math> <math> \tan \alpha = \frac{\sin \alpha}{\sqrt{1 - \sin^2 \alpha} } </math>

योग नियम की व्याख्या

<math> \sin (\alpha - \beta) = \sin \alpha\ \cos \beta - \cos \alpha\ \sin \beta </math>

<math> \sin (\alpha + \beta) = \sin \alpha\ \cos \beta + \cos \alpha\ \sin \beta </math>

<math> \cos (\alpha - \beta) = \cos \alpha\ \cos \beta + \sin \alpha\ \sin \beta </math>

<math> \cos (\alpha + \beta) = \cos \alpha\ \cos \beta - \sin \alpha\ \sin \beta </math>

<math> \tan (\alpha - \beta) = \frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta} </math>

<math> \tan (\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta} </math>

उपरोक्त में यदि α = β रख दें तो,

<math> \sin (2 \alpha) = 2 \sin \alpha \cos \alpha</math>

<math> \cos (2 \alpha) = \cos^2 \alpha- \sin^2 \alpha</math>

<math> \cos (2 \alpha) = 2 \cos^2 \alpha - 1 </math>

<math> \cos (2 \alpha) = 1 - 2 \sin^2 \alpha\ </math>

<math> \tan (2 \alpha) = \frac{ 2 \tan \alpha\ }{ 1 - \tan^2 \alpha\ } </math>

<math> \sin (3 \alpha) = 3 \sin \alpha - 4 \sin^3 \alpha</math>

<math> \cos (3 \alpha) = 4 \cos^3 \alpha - 3 \cos \alpha</math>

<math> \tan (3 \alpha) = \frac{3 \tan \alpha - \tan^3 \alpha}{1 - 3 \tan^2\alpha} </math>

<math>\cos\alpha + \cos\beta = 2\cos \frac{\alpha + \beta}{2}\cos \frac{\alpha - \beta}{2} </math>

<math>\cos\alpha - \cos\beta =-2\sin \frac{\alpha + \beta}{2}\sin \frac{\alpha - \beta}{2} </math>

<math>\sin\alpha + \sin\beta = 2\sin \frac{\alpha + \beta}{2}\cos \frac{\alpha - \beta}{2} </math>

<math>\sin\alpha - \sin\beta = 2\cos \frac{\alpha + \beta}{2}\sin \frac{\alpha - \beta}{2} </math>

<math> \sin \alpha + \cos \alpha = \sqrt{2} \cos \left( \alpha - \tfrac{1}{4}\pi \right) = \sqrt{2}\sin(\alpha+\tfrac{1}{4}\pi)</math>

<math> \sin \alpha - \cos \alpha = -\sqrt{2} \cos \left( \alpha + \tfrac{1}{4}\pi \right) = \sqrt{2}\sin(\alpha-\tfrac{1}{4}\pi) </math>

<math> \cos^2 \alpha = \frac{1 + \cos 2\alpha}{2} </math>

<math> \sin^2 \alpha = \frac{1 - \cos 2\alpha}{2} </math>

<math> \sec^2 \alpha = 1 + \tan^2 \alpha </math>

<math> \sin\alpha\cos\beta = \tfrac{1}{2} \sin (\alpha - \beta) + \tfrac{1}{2} \sin (\alpha + \beta) </math>

<math> \sin\alpha\sin\beta = \tfrac{1}{2} \cos (\alpha - \beta) - \tfrac{1}{2} \cos (\alpha + \beta) </math>

<math> \cos\alpha\cos\beta = \tfrac{1}{2} \cos (\alpha - \beta) + \tfrac{1}{2} \cos (\alpha\ + \beta\ ) </math>

<math>\sin^2\alpha \cos^2\alpha = \frac{1 - \cos(4\alpha)}{8}</math>

त्रिभुज की भुजाओं एवं कोणों में सम्बन्ध

साइन सूत्र

<math>\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R,</math>

जहाँ

<math>R = \frac{abc}{\sqrt{(a+b+c)(a-b+c)(a+b-c)(b+c-a)}}.</math>

कोसाइन सूत्र

<math>c^2=a^2+b^2-2ab\cos C ,</math>

या:

<math>\cos C=\frac{a^2+b^2-c^2}{2ab}.</math>

टैन सूत्र

<math>\frac{a-b}{a+b}=\frac{\mathop{\operatorname{tan}}\left[\tfrac{1}{2}(A-B)\right]}{\mathop{\operatorname{tan}}\left[\tfrac{1}{2}(A+B)\right]}</math>

त्रिकोणमिति के विकास में भारतीय योगदान

आर्यभट

भारतीय गणितज्ञों ने त्रिकोणमिति के क्षेत्र में अत्यन्त महत्वपूर्ण योगदान किया है। आर्यभट (476-550 ई.) ने अपने आर्यसिद्धान्त नामक ग्रन्थ में सबसे पहले ज्या (साइन), कोज्या (कोसाइन), उत्क्रम ज्या (versine) तथा व्युज्या (inverse sine) की परिभाषा की, जिससे त्रिकोणमिति का जन्म हुआ। वस्तुतः आज प्रयुक्त 'साइन' और 'कोसाइन' आर्यभट द्वारा पारिभाषित 'ज्या' और 'कोज्या' के ही बिगडे हुए रूप (अपभ्रंश) हैं। आर्यभट ने ही सबसे पहले साइन और वर्साइन (versine) (1 − cos x) की सारणी प्रस्तुत की है जो 3.75° के अन्तराल पर 0° से 90°तक के कोण के लिए है और दशमलव के चार अंकों तक शुद्ध है। अन्य भारतीय गणितज्ञों ने आर्यभट के कार्य को और आगे बढ़ाया।

६ठी शताब्दी के भारतीय गणितज्ञ वराहमिहिर ने निम्नलिखित सूत्र दिये-

<math>\sin^2 x + \cos^2 x = 1\;</math>

<math>\sin x = \cos\left(\tfrac{\pi}{2} - x\right) </math>

<math>\tfrac{1 - \cos(2x)}{2} = \sin^2 x </math>

७वीं शताब्दी में, भास्कर प्रथम ने एक सूत्र दिया जिसकी सहायता से किसी न्यूनकोण के साइन का सन्निकट (approximate) मान बिना सारणी के निकाला जा सकता है( इस गणना में अशुद्धि 1.9% से भी कम होती है।):

<math>\sin x \approx \tfrac{16x (\pi - x)}{5 \pi^2 - 4x (\pi - x)}, \qquad 0 \leqslant x \leqslant \tfrac{\pi}{2}</math>

७वीं शताब्दी के अन्त में ब्रह्मगुप्त ने निम्नलिखित सूत्र दिए-

<math>\ 1 - \sin^2 x = \cos^2 x = \sin^2\left(\tfrac{\pi}{2} - x \right)</math>

तथा ब्रह्मपुत्र अंतर्वेशन सूत्र (इन्टरपोलेशन फॉर्मूला) यह है-

<math>f( a + x h ) \approx f(a) + x \left(\tfrac{\Delta f(a) + \Delta f(a-h)}{2}\right) + \tfrac{x^2 \Delta^2 f(a-h)}{2}.</math>

जिसकी सहायता से विभिन्न कोणों के साइन के मान निकाले जा सकते थे।. साँचा:clear

त्रिकोणमिति के उपयोग

सूर्य या तारे क्षितिज से कितना कोण बना रहे हैं, यह मापने के लिए सेक्स्टेंट का उपयोग किया जाता है। त्रिकोणमिति तथा समुद्री क्रोनोमीटर का उपयोग करके, इस तरह के माप से जहाज की स्थिति निर्धारित की जा सकती है।

त्रिकोणमिति और त्रिकोणमितीय फलनों के अनेकानेक उपयोग हैं। उदाहरण के लिए, खगोल विज्ञान में त्रिकोणीयन की तकनीक का उपयोग आसपास के तारों की दूरी ज्ञात की जा सकती है। इसी तरह, भूगोल में त्रिकोणीयन द्वारा भू-चिह्नों (लैण्डमार्क) के बीच की दूरी निकाल सकते हैं। उपग्रह की सहायता से नौवहन में त्रिकोणमिति अत्यन्त उपयोगी है। अन्य शब्दों में यह कहा जा सकता है कि जो दूरियाँ सीधे नहीं मापी जा सकती या जिन्हें सीधे मापना अत्यन्त कठिन है, उन दूरियों की गणना त्रिकोणमिति की सहायता से अत्यन्त शुद्धता से की जा सकती है। इसके लिए अत्यन्त सरलता से मापे जा सकने वाली कुछ अन्य दूरियाँ और कोण मापने पड़ते हैं। उदाहरण के लिए किसी वृक्ष की ऊँचाई सीधे मापना कठिन हो तो धरातल पर स्थित किसी बिन्दु से उस वृक्ष की जड़ तक की दूरी तथा उस बिन्दु से वृक्ष के शिखर का कोण माप लिया जाय तो त्रिकोणमितीय गणना द्वारा बड़ी आसानी से उसकी ऊँचाई निकाली जा सकती है। इसी तरह यदि आप किसी नदी के किनारे खड़े हैं और उस नदी की चौड़ाई जानना चाहते हैं तो इसके लिए त्रिकोणमिति की सहायता ले सकते हैं। मान लीजिए कि उस नदी के दूसरे किनारे पर एक मन्दिर है। आप मन्दिर के ठीक सामने नदी के इस किनारे पर खड़े होकर उसके शिखर का उन्नयन कोण माप लीजिए। फिर नदी के इसी किनारे-किनारे कुछ दूरी (जैसे, १०० मीटर) चलने के बाद वहाँ से मन्दिर के शिखर का उन्नयन कोण माप लीजिए। इन दो कोणों और एक दूरी के ज्ञात होने से उस नदी की चौड़ाई निकाल सकते हैं।

सन्दर्भ

इन्हें भी देखें

• त्रिकोणमितीय सर्वसमिकाओं की सूची
• त्रिकोणमिति के उपयोग
• त्रिकोणीय सर्वेक्षण
• प्रतिलोम त्रिकोणमितीय फलन