नियंत्रण प्रणाली

अभिकेन्द्री नियंत्रक (सेन्ट्रिफ्युगल गवर्नर) ; आज की नियंत्रण की भाषा में कहें तो यह एक समानुपाती नियंत्रक (proportional controller) था।

एक औद्योगिक नियंत्रण लूप और उसके विभिन्न अवयव (सेन्सर, ऐक्चुएटर, कन्ट्रोलर आदि)

एक सरल फीडबैक कन्ट्रोल लूप

फीडबैक कन्ट्रोल लूप में प्रायः प्रयुक्त संकेत

किसी तन्त्र के ऑउटपुट या अवस्था-चरों (स्टेट-वैरिएबल्स) को आवश्यकतानुसार बनाये रखने (या परिवर्तित करने) के लिये जो कुछ अतिरिक्त व्यवस्था की जाती है उसे नियन्त्रण प्रणाली (control system) कहते हैं। जिस मूल तन्त्र के ऑउटपुट को नियंत्रित करना होता है, उसे संयंत्र (प्लान्ट) या नियंत्रित तन्त्र कहते हैं। नियन्त्रण प्रणाली, संयंत्र के ऑउटपुट या स्टेट-चरों के मान पर लगातार नजर रखती है तथा संयंत्र के इन्पुट को इस प्रकार बदलती रहती है कि ऑउटपुट वैसा ही बने रहें या वैसे ही बदलें जैसा वांछित हो।

नियंत्रण प्रणाली का महत्व

• नियन्त्रण प्रणाली, इंजीनियरिंग के विकास का मुख्य साधन है।
• औद्योगिक क्रांति वास्तव में स्वचालित नियंत्रण प्रणालियों के कारण ही सम्भव हो सकी थी।
• वायुयान (उड़ने वाली मशीन) के निर्माण की समस्या तभी सुलझी जब १९०३ में राइट बन्धुओं ने उससे सम्बन्धित स्थायित्व एवं नियन्त्रण की समस्या को हल कर लिया।
• मशीनी औजारों के संख्यात्मक नियंत्रण के कारण उत्पादन में वृद्धि और उत्पादन की गुणवत्ता में भारी वृद्धि हुई है।
• रोबोट भी नियन्त्रण प्रणाली के कारण ही इतने उपयोगी सिद्ध हो रहे हैं।

प्रतिपूर्ति नियंत्रण प्रणाली के प्रमुख घटक

• संसूचक (ऑउटपुट सेंसर)
• तुलनाकार, त्रुटि-प्रवर्धक या एरर-एम्प्लिफायर
• नियंत्रक या कम्पन्सेटर (Controller or compensator) या नियंत्रण का अल्गोरिद्म (डिजिटल कन्ट्रोल की दशा में, अर्थात जब नियंत्रक, सॉफ्टवेयर में इम्प्लीमेन्ट किया गया हो)
• नियंत्रित निकाय (कन्ट्रोल्ड सिस्टम) - वह निकाय या प्रक्रम जिसे नियंत्रित किया जा रहा है।

प्रकार

• क्रमिक नियंत्रण (सेक्वेन्शियल कन्ट्रोल) - इसमें नियंत्रण प्रणाली का कार्य, विविध कार्यों को उचित क्रम में लागू करना होता है।

• प्रतिपूर्ति नियंत्रण या फीडबैक कन्ट्रोल - इसमें ऑउटपुट को इष्ट (रिफरेन्स) से तुलना करके इन्पुट की सही ढंग से बदला जाता है ताकि ऑउट्पुट, रिफरेंस के अनुरूप, जैसी जरूरत हो, बदले या स्थिर रहे।

• फजी (Fuzy) नियंत्रण

इसी प्रकार नियंत्रण प्रणाली एनालॉग या डिजिटल हो सकती है। रेखीय या अरेखीय हो सकती है।

सोपानी नियंत्रण

तीन लूपों वाली एक सोपानी नियन्त्रण प्रणाली

सोपानी नियंत्रण (सोपान = सीढ़ी ; cascade control) प्रणाली में एक से अधिक लूप होते हैं। इसमें नियन्त्रण चर के नियन्त्रण के लिये न केवल इसे ही मापा जाता है बल्कि किसी अन्य चर (या कई चरों को) को भी मापा जाता है। नियंत्रण चर को सीधे नियंत्रित करने के बजाय बाहरी लूप, भीतरी लूप के लिये सेट-पॉइन्ट प्रदान करता है जो प्रक्रम के माध्यम से अन्ततः प्राथमिक चर को नियंत्रित करता है।

सोपानी नियन्त्रण चुनने का मुख्य कारण यह होता है कि इससे नियन्त्रण करने में कठिन तन्त्र दो भागों में बंट जाता है और मुख्य डिस्टर्बैंस को घेरते हुए एक द्वितीयक नियन्त्रण लूप बना दिया जाता है। इस प्रकार द्वितीयक लूप अधिकांश डिस्टर्बैंस को हटा देता है अतः मुख्य लूप को केवल छोटी डिस्टर्बैन्स को ही नियन्त्रित करना होता है। 'शीघ्र सूचना (चेतावनी) सफलता का आधार है' (Early Warning is Basis for Success) - यही सोपानी नियंत्रण का भी आधार है।

सोपानी नियन्त्रण के लाभ

• प्राथमिक चर का बेहतर नियन्त्रण
• डिस्टर्बैंस, प्राइमरी चर को कम प्रभावित कर पाते हैं।
• डिस्टर्बेन्स का प्रभाव बहुत जल्दी समाप्त करने में मदद मिलती है।
• सिस्टम की प्राकृतिक आवृत्ति में वृद्धि
• देरी ( time-lag) में कमी
• गतिकीय परफॉर्मैंस (dynamic performance) बेहतर हो जाता है।
• द्वितीयक चर को एक सीमा से आगे जाने से आसानी से रोका जा सकता है।
• सोपानी नियंत्रण प्रणाली का परीक्षण भी आसान होता है।

सोपानी नियन्त्रण वहाँ सबसे अधिक लाभदायक होता है जहाँ भीतरी बन्द लूप सभी डिस्टर्बैंस को और दूसरे ऑर्डर के देरी (lag) को समेट ले ताकि प्राथमिक लूप (बाहरी लूप) में केवल 'बड़ा लैग' ही शामिल हो।

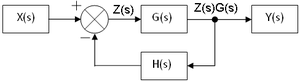
बन्द लूप ट्रान्सफर फलन

बन्द लूप का ट्रान्सफर फलन निम्नलिखित होता है-

<math>\dfrac{Y(s)}{X(s)} = \dfrac{G(s)}{1 + G(s) H(s)}</math>

उपपत्ति

पार्श्व चित्र को देखें। चित्र के अनुसार हम लिख सकते हैं कि,

<math>Y(s) = Z(s)G(s) </math>

<math>Z(s) = X(s)-Y(s)H(s)</math>

<math>X(s) = Z(s) + Y(s)H(s)</math>

<math>X(s) = Z(s) + Z(s)G(s)H(s)</math>

<math>\Rightarrow \dfrac{Y(s)}{X(s)} = \dfrac{Z(s)G(s)}{Z(s) + Z(s)G(s) H(s)}</math>

<math>\dfrac{Y(s)}{X(s)} = \dfrac{G(s)}{1 + G(s) H(s)}</math>

स्वतः नियंत्रण का संक्षिप्त इतिहास

पीआईडी नियंत्रक का ब्लॉक आरेख

PID गुणकों (K_p,K_i,K_d) के मान बदलने पर नियंत्रित प्रणाली के स्टेप सिस्पॉन्स का बदलना

• 1868 नियंत्रण से सम्बन्धित प्रथम लेख ‘on governor’s’ (जे सी मैक्स्वेल द्वारा)। इसमें जेम्स वाट के फ्लाईबाल गवर्नर के गति एवं स्थायित्व का गणितीय विश्लेषण प्रस्तुत किया गया था। नियन्त्रण की गतिकी को अवकल समीकरणों के द्वारा अभिव्यक्त किया गया।
• 1877 रूथ का स्थायित्व कसौटी (Routh stability criterien)
• 1892 लियापुनोव का स्थायित्व निकष (Liapunov stability condition)
• 1895 हर्विट्ज का स्थायित्व निकष (Hurwitz stability condition)
• 1922 मिनोर्स्की ((Minorsky) ने तीन पद वाला PID नियंत्रक विकसित किया।
• 1927 ब्लैक ने नकारात्मक फीडबैक युक्त इलेक्ट्रॉनिक प्रवर्धक का विकास किया। इससे PID नियंत्रकों का प्रयोग करने में बहुत सुविधा मिली।
• 1932 नाइक्विस्ट
• 1945 बोडे
• 1947 निकोल्स
• 1948 मूल बिन्दुपथ (Root locus)
• 1949 विनर ऑप्टिमल कन्ट्रोल अनुसंधान
• 1955 कालमन फिल्टर तथा कंट्रोलिबिलिटी/ऑब्जर्वबिलिटी विश्लेषण
• 1956 कृत्रिम बुद्धि (Artificial Intelligence)
• 1957 बेलमन का ऑप्टिमल और एडप्टिव कन्ट्रोल (Bellman optimal and adaptive control)
• 1962 Pontryagin optimal control
• 1965 फजी समुच्चय (Fuzzy set)
• 1972 विद्यासागर बहु-चर ऑप्टिमल कन्ट्रोल तथा रोबस्ट कंट्रोल
• 1981 Doyle Robust control theory
• 1990 न्यूरो-फजी (Neuro-Fuzzy)

इन्हें भी देखें

• पीआईडी नियंत्रक
• नियंत्रक (नियंत्रण सिद्धान्त)
• नियंत्रण सिद्धान्त
• नियंत्रण इंजिनीयरी
• संख्यात्मक नियंत्रण (न्युमेरिकल कन्ट्रोल)
• प्रोग्रामेबल लॉजिक कन्ट्रोलर या पीएलसी
• अरैखिक नियंत्रण

बाहरी कड़ियाँ

• Semiautonomous Flight Direction - Reference unmannedaircraft.org