पाई
| गणितीय नियतांक π पर लेख श्रृंखला का एक भाग |
| गणितीय नियतांक π |
|---|
| उपयोग |
| चकती का क्षेत्रफल • परिधि • अन्य सूत्रों में प्रयोग |
| गुणधर्म |
| अपरिमेयता • उत्कृष्टता |
| परिमाण |
| २२/७ से कम • सन्निकटन • स्मृतिकरण |
| लोग |
| आर्यभट • आर्किमिडिज़ • लियू हुई • जू चोंग्ज्ही • संगमग्राम के माधव • विलियम जोन्स • जॉन मेचिन • जॉन रिंच • लुडॉल्फ वान स्युलेन |
| इतिहास |
| कालक्रम • पुस्तकें |
| संस्कृति में |
| कानून • π दिवस |
| सम्बंधित विषय |
| वृत का वर्गफलीकरण • बेसल समस्या • फाइनमेन बिन्दु • π से सम्बंधित अन्य विषय |
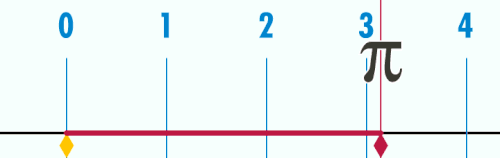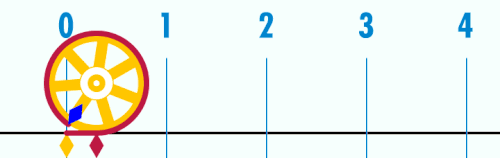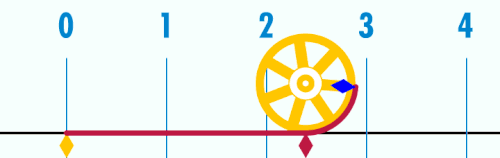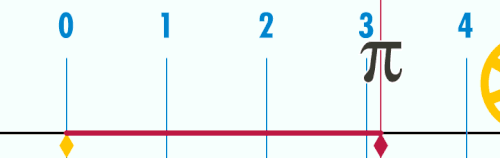
पाई (π) एक गणितीय नियतांक है जिसका संख्यात्मक मान किसी वृत्त की परिधि और उसके व्यास के अनुपात के बराबर होता है। इस अनुपात के लिये π संकेत का प्रयोग सर्वप्रथम सन् १७०६ में आया। इसका मान लगभग 3.14159 के बराबर होता है। यह एक अपरिमेय राशि है।
पाई सबसे महत्वपूर्ण गणितीय एवं भौतिक नियतांकों में से एक है। गणित, विज्ञान एवं इंजीनियरी के बहुत से सूत्रों में π आता है।[१]
इतिहास
पुरातन
2589–2566 ई. पूर्व बने गीजा की महान पिरामिड का परिमाप 1760 क्यूबिट और ऊंचाई 270 क्यूबिट थी; जिसका अनुपात 1760/270 ≈ 6.2757 पाई के मान के लगभग 2 गुणा है। इस अनुपात के आधार पर, कुछ मिस्रविद्य मानते हैं कि पिरामिड बनाने वाले π का ज्ञान रखते थे और वृत के गुणधर्मों को निगमित करने वाले पिरामिड जान - बूझकर बनाए।[२] अन्य मतों के अनुसार π से सम्बंधित उपरोक्त सुझाव केवल संयोग है, क्योंकि इसका कोई प्रमाण उपलब्द्ध नहीं है कि पिरामिड बनाने वालों को π के बारे में जानकारी थी और चूंकि पिरामिड की विमाएं अन्य कारकों पर भी निर्भर करती हैं।[३]
π के शीघ्रातिशीघ्र लिखित सन्निकट मिस्र और बाबिल में मिले हैं, ये दोनों माप १ प्रतिशत की शुद्धता के साथ हैं। बाबिल में ई. पूर्व 1900-1600 दिनांक वाली क्ले गोली पर ज्यामितीय कथन है कि π का निहित अर्थ 25/7=3.12409 है।[४] मिस्र में ई. पूर्व 1650 दिनांकित, en:Rhind Papyrus, परन्तु यह ई. पूर्व 1850 दिनांकित एक लेखपत्र की प्रतिलिपी है जिसमें वृत के क्षेत्रफल का सूत्र दिया गया है जो π को (16/9)2 ≈ 3.1605 के रूप में उपयोग करता है।[४]
भारतीय गणित में पाई
भारत में ई. पूर्व 600 में शुल्ब सूत्रों π को (1785/5568)2 ≈ 3.088 लिखा गया है।[५] ई. पूर्व 259 अथवा शायद इससे भी पहले में भारतीय स्रोत π को <math>\scriptstyle \sqrt{10}</math> ≈ 3.1622 लिखते थे।[६]
आर्यभट ने निम्नलिखित श्लोक में पाई का मान दिया है-
- चतुराधिकं शतमष्टगुणं द्वाषष्टिस्तथा सहस्त्राणाम्।
- अयुतद्वयस्य विष्कम्भस्य आसन्नौ वृत्तपरिणाहः॥
- 100 में चार जोड़ें, आठ से गुणा करें और फिर 62000 जोड़ें। इस नियम से 20000 परिधि के एक वृत्त का व्यास ज्ञात किया जा सकता है।
- ( (100+4)*8+62000/20000=3.1416 )
इसके अनुसार व्यास और परिधि का अनुपात ((4 + 100) × 8 + 62000) / 20000 = 3.1416 है, जो दशमलव के पाँच अंकों तक बिलकुल टीक है।
** इसके अनुसार Circumference और Diameter का अनुपात ((4 + 100) × 8 + 62000) / 20000 = 3.1416 है, जो दशमलव के पाँच अंकों तक बिलकुल ठीक है।[७]
शंकर वर्मन ने सद्रत्नमाला में पाई का मान निम्नलिखित श्लोक में दिया है, जो कटपयादि प्रणाली का उपयोग करके लिखा गया है-
- भद्राम्बुद्धिसिद्धजन्मगणितश्रद्धा स्म यद् भूपगी:
- = 3.1415926535897932384626433832795 (इकतीस दशमलव स्थानों तक।)
कुछ प्रमुख भारतीय गणित ग्रन्थों में पाई के मान निम्नलिखित हैं-[८]
| शुल्बसूत्र | पाई का मान |
|---|---|
| 1) B.SI. 1-113 | 3 |
| 2) M.SI. 1.27 | 3.16049 |
| 3) M.SI. (मजुमदार) | 2.99, 3.029 |
| 4) M.SI. 10.1.1.8 | 3.088 |
| 5) M.Si. 10.1.8 | 3.308 |
| 6) K.SI. 3-13 | 3.0852 |
| 7) K.SI. 3-14 | 3.004 |
| 8) B.SI. 1-60 | 3.004 |
| 9) B.SI. 1-59 | 3.0971 |
| 10) द्वारकानाथ यज्वा | 3.157991 |
| 11) आर्यभटीयम् 2-10 | 3.1416 |
| 12) B.SI. 2-10 | 3.14159 |
| 13) लीलावती (p-277) | 3.1415926535 |
| 14) K.SI. 3-13 | 3.088 |
| 15) B.SI. 16-6-11 | 3.114 |
सन्दर्भ
इन्हें भी देखें
बाहरी कड़ियाँ
- Pi in Indian Mathematics
- Formulas for π at MathWorld
- Representations of Pi at Wolfram Alpha
- Pi स्क्रिप्ट त्रुटि: "webarchive" ऐसा कोई मॉड्यूल नहीं है। at PlanetMath
- Determination of π at Cut-the-knot
- Statistical Distribution Information on PI स्क्रिप्ट त्रुटि: "webarchive" ऐसा कोई मॉड्यूल नहीं है। based on 1.2 trillion digits of PI
- ↑ साँचा:cite book
- ↑ "हम यह निष्कर्ष निकाल सकते हैं यद्यपि प्राचीन मिस्रविद्यों के अनुसार π का शुद्ध मान नहीं प्राप्त किया जा सकता, व्यवहारिक जीवन में उन्होनें इसका प्रयोग किया।" साँचा:cite document, p. 70.
साँचा:cite document, p. 30.
See also साँचा:cite journal.
See also साँचा:cite journal - ↑ मिस्रविद्य: रोजी, कोरिन्ना, Architecture and Mathematics in Ancient Egypt, Cambridge University Press, 2004, pp 60–70, 200, ISBN 9780521829540.
Skeptics: Shermer, Michael, The Skeptic Encyclopedia of Pseudoscience, ABC-CLIO, 2002, pp 407–408, ISBN 9781576076538.
See also Fagan, Garrett G., Archaeological Fantasies: How Pseudoarchaeology Misrepresents The Past and Misleads the Public, Routledge, 2006, ISBN 9780415305938.
For a list of explanations for the shape that do not involve साँचा:pi, see स्क्रिप्ट त्रुटि: "citation/CS1" ऐसा कोई मॉड्यूल नहीं है। - ↑ अ आ साँचा:harvnb
- ↑ साँचा:harvnb
- ↑ साँचा:harvnb
- ↑ How Aryabhata got the earth's circumference right साँचा:webarchive
- ↑ Value of Pi in Some mathematical calculations in various texts
