वृत्त

| |
| तल | द्विविमीय |
| अर्थ | केंद्र से समान दूर होने वाले बिंदुओं का समूह |
| व्यास | केंद्र से होकर जाने वाली जीवा |
| त्रिज्या | अर्द्धव्यास |
| परिधि | परिधि = π x व्यास |
किसी एक निश्चित बिंदु से समान दूरी पर स्थित बिंदुओं का बिन्दुपथ वृत्त कहलाता है। यह निश्चित बिंदु, वृत्त का केंद्र कहलाता है, केंद्र और वृत्त की परिधि के किसी भी बिन्दु के बीच की दूरी वृत्त की त्रिज्या कहलाती है। वृत्त एक साधारण बंद वक्र होता है जो समतल को दो क्षेत्रों में विभाजित करता है: एक आंतरिक और एक बाहरी।
वृत्त एक प्रकार का शांकव (शंकु परिच्छेद) होता है जिसकी उत्केंद्रता (Eccentricity) शून्य होती है अर्थात नियता (Directrix) समतल में अनंत पर स्थित होती है। एक वृत्त को एक विशेष प्रकार के दीर्घवृत्त के रूप में भी परिभाषित किया जा सकता है जिसमें दोनों नाभियाँ (Focii) संपाती होती हैं और उत्केन्द्रता 0 होती है। यूक्लिड के अनुसार, 'वृत्त एक रेखा से घिरा हुआ एकविमीय समतल होता है और किसी निश्चित बिंदु से लेकर उस बंधरेखा तक खींची गई सभी रेखाएं बराबर होती हैं। इस बंधरेखा को परिधि और इस निश्चित बिंदु को वृत्त का केंद्र कहते हैं।'
यूक्लिड की परिभाषा
वृत्त एक बंधरेखा से घिरी हुई एक समतलीय आकृति है, और यह इस तरह होता है कि किसी निश्चित बिंदु इस बंधरेखा तक की सभी रेखाएं लंबाई में बराबर होता हैं। यह बंधरेखा, इस वृत्त की परिधि और निश्चित बिंदु, इसका केंद्र कहलाता है।
शब्दावली
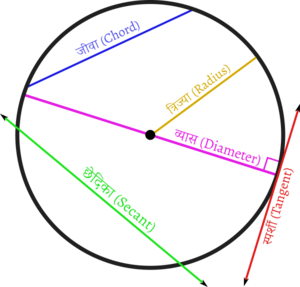
चाप (Arc): वृत्त की परिधि का कोई भी भाग।
केंद्र (Centre): वृत्त पर स्थित सभी बिंदुओं से समदूरस्थ बिंदु।
जीवा (Chord): एक रेखाखंड, जो वृत्त पर स्थित किन्हीं दो बिन्दुओं को मिलने पर बनता है। एक जीवा वृत्त को दो वृत्तखंडों में विभाजित करती है।
परिधि (Circumfrence): वृत्त के चारों ओर की वक्र लंबाई।
व्यास (Diameter): एक रेखाखंड जिसके अंतबिन्दु वृत्त पर स्थित होते हैं और जो केंद्र से गुजरता है या वृत्त के किन्हीं दो बिंदुओं के बीच की अधिकतम दूरी है। यह वृत्त की सबसे बड़ी जीवा होती है और यह त्रिज्या की दोगुनी होती है।
डिस्क (Disc): एक वृत्त से घिरा अन्तः समतलीय क्षेत्र।
त्रिज्या (Radius): वृत्त के केंद्र से वृत्त की परिधि के किसी भी बिंदु तक का एक रेखाखंड, जो व्यास का आधा होता है।
त्रिज्यखंड (Sector): किन्हीं दो त्रिज्याओं के बीच एक चाप से घिरा क्षेत्र।
वृत्तखण्ड (Segment): केंद्ररहित एक क्षेत्र जो वृत्त की एक जीवा और एक चाप से घिरा होता है। एक जीवा वृत्त को दो वृत्तखंडों में विभाजित करती है।
छेदन रेखा या छेदिका (Secant): एक विस्तारित जीवा, जो वृत्त के समतलीय होती है तथा वृत्त को दो बिन्दुओं पर प्रतिच्छेदित करती है।
स्पर्शी या स्पर्श रेखा (Tangent): वृत्त के समतलीय सीधी रेखा जो एक बिंदु पर वृत्त को स्पर्श करती है।
अर्धवृत्त (Semicircle): वृत्त के व्यास तथा व्यास के अंतबिन्दुओं से बने चाप के मध्य का क्षेत्र अर्धवृत्त होता है। अर्धवृत्त का क्षेत्रफल, वृत्त के सम्पूर्ण क्षेत्रफल का आधा होता है।
वृत्त की स्पर्श रेखा के गुण
(a) वृत्त के एक बिन्दु पर एक और केवल एक स्पर्श रेखा होती है।
(b) किसी वृत्त की स्पर्श रेखा छेदक रेखा की एक विशिष्ट दशा है जब संगत जीवा के दोनों सिरे संपाती हो जाएँ।
(c) स्पर्श रेखा और वृत्त के कॉमन प्वांट (उभनिष्ठ बिन्दु) को स्पर्श बिन्दु (point of contact) कहते हैं। तथा स्पर्श रेखा को वृत के उभयनिष्ठ बिन्दु पर स्पर्श करना कहते हैं।
(d) वृत्त के अंदर स्थित किसी बिन्दु से जाने वाली वृत्त पर कोई स्पर्श रेखा नहीं है।
(e) वृत्त पर स्थित किसी बिन्दु से वृत्त पर एक और केवल एक स्पर्श रेखा है।
(f) वृत्त के बाहर स्थित किसी बिन्दु से जाने वाली वृत्त पर दो और केवल दो स्पर्श रेखाएँ हैं।
(g) बाह्य बिन्दु P से वृत के स्पर्श बिन्दु तक स्पर्श रेखा खंड की लम्बाई को बिन्दु P से वृत्त पर स्पर्श रेखा की लम्बाई कहते हैं।
विश्लेषणात्मक परिणाम
परिधि की लंबाई:[१]
वृत्त की परिधि तथा उसके व्यास का अनुपात π (पाई) होता है, जिसका मान लगभग 3.141592654 के बराबर है। इस प्रकार परिधि की लंबाई C, त्रिज्या r और व्यास d से निम्न प्रकार संबंधित है:
<math>C=2\pi r=\pi d</math>
क्षेत्रफल:
आर्किमिडीज ने वृत्त के क्षेत्रफल मापन में सिद्ध किया कि एक वृत्त का क्षेत्रफल, एक त्रिभुज के क्षेत्रफल के बराबर है, जिसका आधार वृत्त की परिधि की लंबाई के बराबर और इसकी ऊंचाई वृत्त की त्रिज्या के बराबर होती है। अतः π तथा त्रिज्या के वर्ग का गुणनफल, वृत्त के क्षेत्रफल के बराबर होता है।
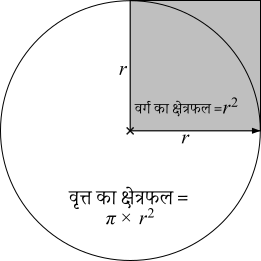
क्षेत्रफल <math>\mathrm {A} =\pi r^{2}.\,</math>
यदि वृत्त का व्यास d हो तब,
क्षेत्रफल <math>\mathrm {A} ={\frac {\pi d^{2}}{4}}\approx 0{.}7854d^{2},</math>
यह वर्ग के क्षेत्रफल के लगभग 79% के बराबर है जिसकी भुजा की लंबाई d है।
समीकरण
कार्तीय निर्देशांक
- वृत्त का समीकरण
एक x-y कार्तीय निर्देशांक प्रणाली में, केंद्र (a,b) और त्रिज्या r के वृत्त का समीकरण
<math>\left(x-a\right)^{2}+\left(y-b\right)^{2}=r^{2}.</math>
वृत्त के समीकरण के रूप में जाना जाने वाला यह समीकरण, पाइथागोरियन प्रमेय से वृत्त पर स्थित सभी बिंदुओं पर लागू होता है: जैसा कि आसन्न आरेख में दिखाया गया है, वृत्त की त्रिज्या, एक समकोण त्रिभुज का कर्ण (hypotenuse) है जिसकी अन्य भुजाओं की लंबाई |x - a| और |y - b| हैं।यदि वृत्त का केंद्र मूलबिंदु (0,0) तथा त्रिज्या r हो तब वृत्त का समीकरण:
<math>x^{2}+y^{2}=r^{2}.\!\ </math>
- प्राचलिक रूप
त्रिकोणमितीय फलन ज्या (sine) और कोज्या (cosine) का प्रयोग करके प्राचलिक रूप में वृत्त के समीकरण को निम्नलिखित रूप में लिखा जा सकता है-
<math>x=a+r\,\cos t,\, </math>
<math>y = b+r\,\sin t\,</math>
जहाँ t, 0 से 2π श्रेणी का प्राचल है, जो (a, b) से (x, y) तक किरण द्वारा धनात्मक x-अक्ष के साथ बनाये गए कोण की ज्यामितीय रूप में व्याख्या करता है।
- वृत्त का एक वैकल्पिक प्राचलीकरण निम्नलिखित है-
<math>{\displaystyle x=a+r{\frac {1-t^{2}}{1+t^{2}}}.\,}</math>
<math>{\displaystyle y=b+r{\frac {2t}{1+t^{2}}}\,}</math>
इस प्राचलीकरण में, अनुपात t : r, वृत्त के केंद्र से गुजरने वाली तथा x-अक्ष के समांतर रेखा के स्टीरियोग्राफिक प्रक्षेपण (Stereo graphic Projection) के रूप में ज्यामितीय व्याख्या करता है।
- यदि वृत्त के किसी व्यास के सिरों के निर्देशांक <math>{\displaystyle (x_{1},y_{1})}</math>व <math>{\displaystyle {\displaystyle (x_{2},y_{2})}} </math>हों, तब वृत्त का समीकरण निम्न होता है:
<math>{\displaystyle (x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})=0}</math>
प्रमुख गुण
- वृत्त के व्यास द्वारा परिधि के किसी भी बिंदु पर अंतरित कोण समकोण (90 अंश) होता है।
- जीवा पर केन्द्र से डाला गया लम्ब उस जीवा का समद्विभाजक भी होता है।
- चक्रीय चतुर्भुज के सम्मुख कोणों का योग 180 अंश होता है।
- किसी बाह्य बिदु से वृत्त पर दो स्पर्शरेखाएँ खिंची जा सकतीं हैं। ये दोनों स्पर्शरेखाएँ समान लम्बाई की होती हैं।
वृत्त की जीवा के गुण
- केंद्र से होकर जाने वाली जीवा उस वृत्त की सबसे बड़ी जीवा होती है। इसे 'व्यास' (Diameter) कहते हैं।
- किसी वृत्त का व्यास उस वृत्त को दो सामान भागों में विभक्त करता है।
- व्यास, त्रिज्या का दोगुना होता है। व्यास = 2 (त्रिज्या)
- किसी वृत्त में केंद्र से समान दूरी पर खींची गयी जीवाओं की लंबाई सामान होती है।
- किसी वृत्त में सामान लंबाई की जीवाएं केंद्र से सामान दूरी पर होती हैं।
- ↑ 10th maths