अभिकेन्द्रीय बल
साँचा:asbox जब कोई वस्तु किसी वृत्ताकार मार्ग पर चलती है, तो उस पर कोई एक वृत्त के केंद्र पर बल कार्य करता है, इस बल को अभिकेंद्रीय बल कहते हैं। इस बल के अभाव में वस्तु वृत्ताकार मार्ग पर नहीं चल सकती है। यदि कोई m द्रव्यमान का पिंड v से r त्रिज्या के वृत्तीय मार्ग पर चल रहा है तो उस पर कार्यकारी वृत्त के केंद्र की ओर आवश्यक अभिकेंद्रीय बल f=mv2/r होता है।
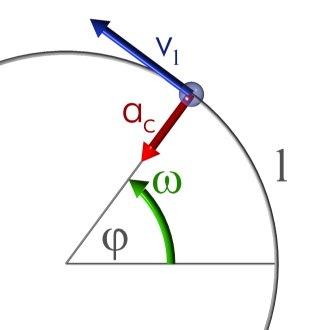
किसी पिण्ड के तात्क्षणिक वेग के लम्बवत दिशा में गतिपथ के केन्द्र की ओर लगने वाला बल 'अभिकेन्द्रीय बल (Centripetal force) कहलाता है। अभिकेन्द्र बल के कारण पिण्ड वक्र-पथ पर गति करती है (न कि रैखिक पथ पर)। उदाहरण के लिये वृत्तीय गति का कारण अभिकेन्द्रीय बल ही है।
<math> \mathbf{a} = -\frac{v^2}{r} \left (\frac{\mathbf{r}}{r}\right) = -\frac{v^2}{r}\hat{\mathbf u}_r = - \omega^2 \mathbf{r} </math>
जहाँ:
- <math> \mathbf{a} \,</math> अभिकेंद्रीय त्वरन है,
- <math> v \,</math> वेग का परिमाण (magnitude) है,
- <math> r \,</math> पथ की वक्रता त्रिज्या है,
- <math> \mathbf{r} \,</math> स्थिति सदिश है,
- <math> \mathbf{u}_r \,</math> त्रिज्य सदिश है,
- <math> \omega \,</math> कोणीय वेग है।
न्यूटन के गति के द्वितीय नियम के अनुसार यदि कहीं कोई त्वरण है तो त्वरण की दिशा में बल अवश्य लग रहा होगा। अतः यदि m द्रव्यमान का कण एकसमान वृत्तीय गति कर रहा हो तो उस पर लगने वाले अभिकेन्द्रीय बल का मान निम्नलिखित सूत्र द्वारा दिया जायेगा:
<math> \mathbf{F} = - \frac{m v^2}{r}\hat{\mathbf u}_r = - m \omega^2 \mathbf{r} </math> इलेक्टोन नाभिक के चारो ओर अभिके्न्दीय बल के कारण चक्कर लगाते है !