सिसैरा-संकलन
गणितीय विश्लेषण में, सिसैरो संकलन सामान्य अर्थों में अभिसरण नहीं करने वाले अनन्त संकलन को मान निर्दिष्ट करता है जो मानक संकलन के साथ सन्निपतित होता है यदि वह अभिसारी हो। सिसैरा संकलन श्रेणी के आंशिक संकलन के समान्तर माध्य के सीमान्त मान के रूप में परिभाषित होता है।
सिसैरा संकलन का नामकरण इतालवी विश्लेषक अर्नेस्टो सिसैरा (1859–1906) के सम्मान में रखा गया।
परिभाषा
माना {an} एक अनुक्रम है और माना
- <math>s_k = a_1 + \cdots + a_k</math>
श्रेणी का kवाँ आंशिक संकलन है
- <math>\sum_{n=1}^\infty a_n.</math>
श्रेणी <math>\sum_{n=1}^\infty a_n</math> सिसैरा योग <math>A \in \R</math> के साथ सिसैरा संकलनीय कहलाती है यदि इसके आंशिक संकलनों के योग का माध्य <math>s_k</math>, <math>A</math> की ओर अग्रसर हो:
- <math>\lim_{n\to\infty} \frac{1}{n}\sum_{k=1}^n s_k = A.</math>
अन्य शब्दों में, किसी अनन्त श्रेणी का सिसैरा संकलन श्रेणी के प्रथम n आंशिक संकलनों का समान्तर माध्य (औसत) का सीमान्त मान होता है जबकि n अनन्त की ओर अग्रसर हो। यह सिद्ध किया जा सकता है कि अभिसारी श्रेणी सिसैरा संकलनीय होती है और श्रेणी का कुल योग सिसैरा संकलन के समान होता है। हालांकि, निम्नलिखित उदाहरण उल्लिखीत करता है कि श्रेणी अपसारी है लेकिन सिसैरा संकलनीय है।
उदाहरण
माना n ≥ 1 के लिए an = (−1)n+1 है। अर्थात {an} एक अनुक्रम है
- <math>1, -1, 1, -1, \ldots.\,</math>
और माना G एक श्रेणी <math> \sum_{n=1}^\infty a_n =1-1+1-1+1-\cdots </math> को निरुपित करता है।
तब आंशिक संकलनों {sn} <math> = \sum_{k=1}^n a_k </math> का अनुक्रम निम्नलिखित होगा
- <math>1, 0, 1, 0, \ldots,\,</math>
इस श्रेणी G को ग्रांडी श्रेणी के रूप में जाना जाता है जो अभिसारी नहीं है। अन्य रूप में, {sn} के पदों के (आंशिक) माध्य अनुक्रम {tn} है जहाँ
- <math> t_n = \frac{1}{n}\sum_{k=1}^n s_k </math>
निम्न प्रकार हैं
- <math>\frac{1}{1}, \,\frac{1}{2}, \,\frac{2}{3}, \,\frac{2}{4}, \,\frac{3}{5}, \,\frac{3}{6}, \,\frac{4}{7}, \,\frac{4}{8}, \,\ldots,</math>
अतः
- <math>\lim_{n\to\infty} t_n = 1/2.</math>
इसलिए श्रेणी G का सिसैरा संकलन का मान 1/2 है।
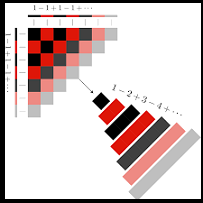
अन्य रूप में, माना n ≥ 1 के लिए an = n है। अर्थात {an} एक अनुक्रम है।
- <math>1, 2, 3, 4, \ldots.\,</math>
और माना G एक श्रेणी <math> \sum_{n=1}^\infty a_n =1+2+3+4+5+\cdots </math> को निरुपित करता है।
तब {sn} के आंशिक संकलनों का अनुक्रम
- <math>1, 3, 6, 10, \ldots,\,</math>
होगा और G का मान अनन्त की ओर अपसरित होगा।
{tn } के आंशिक संकलनों के माध्य के अनुक्रम के पद निम्न प्रकार होंगे:
- <math>\frac{1}{1}, \,\frac{4}{2}, \,\frac{10}{3}, \,\frac{20}{4}, \,\ldots.</math>
अतः, यह अनुक्रम G की तरह अनन्त की ओर अपसरण करता है तथा अब G सिसैरा संकलनीय नहीं है।