संरचनात्मक विश्‍लेषण

लोड के कारण भौतिक संरचनाओं तथा उनके विभिन्न भागों पर पड़ने वाले प्रभाव की गणना करना संरचनात्मक विश्‍लेषण (Structural analysis) कहलाता है। भवन, पुल, वाहन, मशीनें, फर्नीचर, जैव उत्तक आदि सभी में संरचनात्मक विश्लेषण करने की आवश्यकता पड़ सकती है।

संरचनात्मक विश्लेषण के अन्तर्गत प्रयुक्त यांत्रिकी, पदार्थ विज्ञान, तथा अनुप्रयुक्त गणित का उपयोग होता है। इनका प्रयोग करते हुए संरचना की विकृतियों, आन्तरिक बलों, प्रतिबलों, सपोर्ट की प्रतिक्रियाओं, त्वरण तथा स्थायित्व आदि की गणना की जाती है। इस गणना से यह जाँचा जाता है कि कोई संरचना उपयोग के योग्य है या नहीं। संरचनात्मक विश्लेषण करके भौतिक जाँचों से बचा जा सकता है। अतः संरचनाओं के डिजाइन के लिए संरचनात्मक विश्लेषण की महती भूमिका है।

उदाहरण

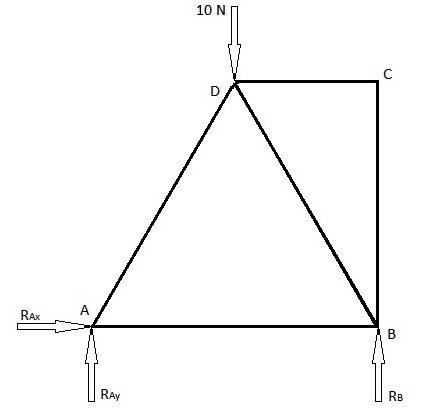
ट्रस के अवयवों में प्रतिबल की गणना करने की दो विधियाँ हैं- (१) संधि की विधि (Method of Joints) तथा (२) परिच्छेद की विधि (Method of Sections)। नीचे एक उदाहरण दिया गया है जिसमें इन दोनों विधियों द्वारा हल निकाला गया है। नीचे दिया गया चित्र सबसे पहले समस्या का परिचय कराता है। इसमें हमे ट्रस के अवयवों में प्रतिबल (स्ट्रेस) निकालना है। दूसरा चित्र, लोडिंग आरेख है जिसमें जोड़ों पर लगने वाली प्रतिक्रियाएँ (रिएक्शन्स) दिखाए गए हैं।

चूंकि बिन्दु A पर एक पिन-सन्धि है, अतः यहाँ दो प्रतिक्रिया बल लगाए जाँएंगे- एक बल x-दिशा में और दूसरा y-दिशा में। बिन्दु B पर रोलर-सन्धि है अतः यहाँ केवल एक प्रतिक्रिया बल लगेगा (y-दिशा में)।

चूंकि यह तन्त्र स्थैतिक संतुलन (static equilibrium) की अवस्था में है, किसी भी दिशा में लगने वाले सभी बलों का (सदिश) योग शून्य होगा; तथा किसी भी बिन्दु के सापेक्ष सभी बलों के आघूर्णोम का योग भी शून्य होगा। इस प्रकार प्रतिक्रिया बलों का परिमाण और दिशा निकाली जा सकेगी।

<math>\sum M_A=0=-10*1+2*R_B \Rightarrow R_B=5</math>

<math>\sum F_y=0=R_{Ay}+R_B-10 \Rightarrow R_{Ay}=5</math>

<math>\sum F_x=0=R_{Ax}</math>

सन्धि विधि

This type of method uses the force balance in the x and y directions at each of the joints in the truss structure.

At A,

<math>\sum F_y=0=R_{Ay}+F_{AD}\sin(60)=5+F_{AD}\frac{\sqrt{3} }{2} \Rightarrow F_{AD}=-\frac{10}{\sqrt{3}}</math>

<math>\sum F_x=0=R_{Ax}+F_{AD}\cos(60)+F_{AB}=0-\frac{10}{\sqrt{3} }\frac{1}{2}+F_{AB} \Rightarrow F_{AB}=\frac{5}{\sqrt{3}}</math>

At D,

<math>\sum F_y=0=-10-F_{AD}\sin(60)-F_{BD}\sin(60)=-10-\left(-\frac{10}{\sqrt{3}}\right)\frac{\sqrt{3} }{2}-F_{BD}\frac{\sqrt{3}}{2} \Rightarrow F_{BD}=-\frac{10}{\sqrt{3}}</math>

<math>\sum F_x=0=-F_{AD}\cos(60)+F_{BD}\cos(60)+F_{CD}=-\frac{10}{\sqrt{3}}\frac{1}{2}+\frac{10}{\sqrt{3} }\frac{1}{2}+F_{CD} \Rightarrow F_{CD}=0</math>

At C,

<math>\sum F_y=0=-F_{BC} \Rightarrow F_{BC}=0</math>

Although we have found the forces in each of the truss elements, it is a good practice to verify the results by completing the remaining force balances.

<math>\sum F_x=-F_{CD}=-0=0 \Rightarrow verified</math>

At B,

<math>\sum F_y=R_B+F_{BD}\sin(60)+F_{BC}=5+\left(-\frac{10}{\sqrt{3}}\right)\frac{\sqrt{3} }{2}+0=0 \Rightarrow verified</math>

<math>\sum F_x=-F_{AB}-F_{BD}\cos(60)=\frac{5}{\sqrt{3}}-\frac{10}{\sqrt{3}}\frac{1}{2}=0 \Rightarrow verified</math>

सेक्सन्स की विधि

प्रथम विधि : दाहिने पक्ष पर ध्यान मत दो (Ignore the right side)

<math>\sum M_D=0=-5*1+\sqrt{3}*F_{AB} \Rightarrow F_{AB}=\frac{5}{\sqrt{3} }</math>

<math>\sum F_y=0=R_{Ay}-F_{BD}\sin(60)-10=5-F_{BD}\frac{\sqrt{3}}{2}-10 \Rightarrow F_{BD}=-\frac{10}{\sqrt{3}}</math>

<math>\sum F_x=0=F_{AB}+F_{BD}\cos(60)+F_{CD}=\frac{5}{\sqrt{3}}-\frac{10}{\sqrt{3}}\frac{1}{2}+F_{CD} \Rightarrow F_{CD}=0</math>

द्वितीय विधि : बाएँ पक्ष पर ध्यान मत दो (Ignore the left side)

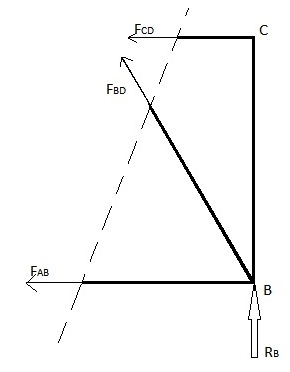
<math>\sum M_B=0=\sqrt{3}*F_{CD} \Rightarrow F_{CD}=0</math>

<math>\sum F_y=0=F_{BD}\sin(60)+R_B=F_{BD}\frac{\sqrt{3}}{2}+5 \Rightarrow F_{BD}=-\frac{10}{\sqrt{3}}</math>

<math>\sum F_x=0=-F_{AB}-F_{BD}\cos(60)-F_{CD}=-F_{AB}-\left(-\frac{10}{\sqrt{3}}\right)\frac{1}{2}-0 \Rightarrow F_{AB}=\frac{5}{\sqrt{3}}</math>

शेष बचे ट्रस के अवयवों में प्रतिबल उपरोक्त विधि से निकाला जा सकता है। इसके लिए अन्य अवयवों से होकर जाने वाला परिच्छेद (सेक्शन) चुनें।

इन्हें भी देखें

• संरचना इंजीनियरी