बोडे आरेख

प्रथम आर्डर के बटरवर्थ फिल्टर का बोडी आलेख

किसी रैखिक काल-अपरिवर्तित प्रणाली के अन्तरण प्रकार्य की आवृत्ति के सापेक्ष आलेख बोडे आलेख या 'बोडे प्लॉट' (Bode plot) कहलाता है। इसमें आवृत्ति-अक्ष लघुगणकीय-पैमाने (log-scale) में होती है। बोडे प्लॉट वस्तुतः किसी प्रणाली का आवृत्ति अनुक्रिया (फ्रेक्वेंसी रिस्पांस) को निरूपित करती है। बोडी प्लॉट प्रायः दो आलेख होते हैं -

आवृति के संगत परिमाण का आलेख, तथा
आवृति के संगत कला (फेज) का आलेख

इस आलेख का नाम संयुक्त राज्य अमेरिका के बेल प्रयोगशाला के प्रसिद्ध नियंत्रक अभियंता हेंड्रिक वाडे बोडे (Hendrik Wade Bode (1905–1982)) के नाम पर पड़ा है। उन्होने १९३० के दशक में लब्धि (gain) और कला (फेज) को प्लॉट करने की एक अत्यन्त सरल किन्तु परिशुद्ध विधि बतायी। नियंत्रण प्रणालियों के विश्लेषण तथा डिजाइन के लिये इस आलेख का बहुत उपयोग होता है। कम्प्यूटर प्रोग्रामों के आ जाने से आजकल यह काम और भी आसान हो गया है।

मूल अवयवों के बोडी आलेख

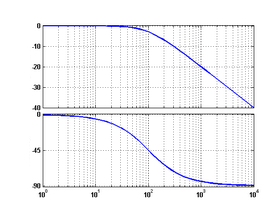
नीचे अंतरण फलनों में प्रायः आने वाले कुछ मूल अवयवों के बोडी आलेख दिये गये हैं। प्रत्येक चित्र में उपर वाला आलेख परिमाण का आलेख है (डेसीबेल में) तथा उसके नीचे का आलेख कला (डिग्री में) का है। क्षैतिक अक्ष कोणीय आवृति w (रेडियन प्रति सेकेण्ड) है।

<math>\omega \, = 2 \;\pi\;f</math>.

क्रमांक	नाम	अन्तरण फलन	टिप्पणी
1	स्थिरांक या समानुपाती अवयव	<math> \ K </math>	<math> \ K = 100 </math>
2	समाकलन अवयव	<math>\frac{1}{s}</math>
3	अवकलन अवयव	<math> \ s </math>
4	प्रथम आर्डर की जड़ता वाला अवयव	<math>\frac{1}{Ts+1}</math>	<math>\ T = 0,01 </math>
5	द्वितीय आर्डर का अल्प-अवमंदित प्रणाली	<math>\frac{1}{T^2s^2 + 2\;\xi\ T s + 1}</math>	<math>\ T = 0,01 </math> <math>\xi\ = 0,1</math>
6	देरी अवयव (डीले एलिमेंट)	<math> \ e^{-sT} </math>	<math>\ T = 0,0001 </math>