गोलीय दर्पण
गोलीय दर्पण (spherical mirror) वे दर्पण हैं जिनका परावर्तक तल गोलीय होता है।
ये दो तरह के होते हैं -
- उत्तल दर्पण (convex mirror / कान्वेक्स मिरर) -- जिस दर्पण का परावर्तक तल बाहर की तरफ उभरा रहता है उसे उत्तल दर्पण कहते हैं।
- अवतल दर्पण (concave mirror / कॉनकेव मिरर) -- जिस दर्पण का परावर्तक तल अन्दर की तरफ दबा हुआ होता है उसे अवतल दर्पण कहते हैं।
कुछ दर्पण ऐसे भी उपयोग किये जाते हैं जिनका परावर्तक तल समतल या गोलीय न होकर किसी अन्य रूप का होता है, जैसे परवलयाकार (parabolic reflectors)। इनका उपयोग परावर्तक दूरदर्शी आदि प्रकाशीय उपकरणों में किया जाता है। इनके उपयोग से गोलीय दर्पणों में पायी जाने वाली 'गोलीय विपथन' की समस्या से छुटकारा मिल जाता है।
गोलीय दर्पण की फोकस दूरी उसकी वक्रता त्रिज्या की आधी होती है
- f=r/2
प्रतिविम्ब
| वस्तु की स्थिति (S), फोकस बिन्दु (F) |
प्रतिविम्ब (Image) | चित्र |
|---|---|---|
| <math>S<F</math> (Object between focal point and mirror) |
|
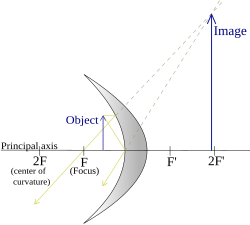
|
| <math>S=F</math> (Object at focal point) |

| |
| <math>F<S<2F</math> (Object between focus and centre of curvature) |
|

|
| <math>S=2F</math> (Object at centre of curvature) |
|

|
| <math>S>2F</math> (Object beyond centre of curvature) |
|

|
अगोलीय (Non-spherical) दर्पण
गोलीय दर्पणों से विपथनमुक्त (unaberrated) बिंब केवल उनके वक्रताकेंद्र पर ही बनता है। प्राय: अन्य सभी शंकुकाटों (conic sections) के इसी प्रकार के प्रकाशीय गुण होते हैं और इन्हीं गुणों के आधार पर उनका प्रकाशीय महत्व नियत किया जाता है। परवलय (parabola) का गुण होता है कि उसके फोकस से चलने वाली सभी किरणें परावर्तन के उपरांत अक्ष के समांतर चली जाती हैं। इस गुण के उपयोगार्थ परवलयज (paraboloidal) दर्पणों का निर्माण किया जाता है। अत्यंत दीर्घ बिंबांतरों (image distances) के लिए इनका उपयोग किया जाता है।
इसी प्रकार दीर्घवृत्त (ellipse) के इस ज्यामितीय गुण का, कि इसके एक फोकस पर स्थित वस्तु का सुतीक्ष्ण बिंब दूसरे फोकस पर बनता है, उपयोग दीर्घवृत्तजीय (ellipsoidal) दर्पण के निर्माण में किया जाता है। लगभग यही विशेषता अतिपरवलयज (Hyprboloidal) दर्पण में भी पाई जाती है। अंतर इतना मात्र होता है कि दीर्घवृत्तजीय दर्पणों में काल्पनिक वस्तु का बिंब प्रतीयमान और वास्तविक वस्तु का बिंब वास्तविक होता है, किंतु अतिपरवलयज दर्पणों द्वारा वास्तविक वस्तु का प्रतीयमान बिंब और काल्पनिक वस्तु का वास्तविक बिंब बन जाता है।
उच्चसामर्थ्य संपन्न दूरदर्शियों (telescopes) तथा अन्य अनेक प्रकाशीय यंत्रों में दर्पणों का उपयोग किया जाता है। दुर्गम चोटियों, शिखरों एव आकाशीय पिंडों की ऊँचाइयाँ नापने के लिए व्यवहृत यंत्र, सेक्सटैंट (sextant), में समतल दर्पणों का उपयोग होता है। विशेषकर सुदीर्घ फोकस अंतरवाली प्रकाश-यंत्र-प्रणालियों में परवलयज, दीर्घवृत्तजीय तथा अतिपरवलयज दर्पणों का उपयोग किया जाता है। इनके कुछ दृष्टांत निम्नलिखित हैं:
न्यूटनीय दूरदर्शी (Newtonian telescope) में परवलयज दर्पण का प्रयोग किया जाता है।
कैसिग्रेनीय (Cassegranian) दूरदर्शी में एक परवलयज तथा एक अतिपरवलयज दर्पण परस्पर इस प्रकार स्थित रहते हैं कि अतिपरवलयज का एक फोकस तो परवलयज के एक फोकस पर पड़ता है और दूसरा फोकस परवलयज के निकट ही स्थित होता है। फलस्वरूप, परवलयज द्वारा निर्मित प्रतीयमान बिंब अतिपरवलयज द्वारा वास्तविक बिंब में परिणत कर दिया जाता है।
ग्रेगोरियन (Gregorian) दूरदर्शी में एक दीर्घवृत्तजीय तथा एक परवलयज दर्पण का प्रयोग होता है। दीर्घवृत्तजीय को परवलयज के फोकस बिंदु से काफी दूर पर रखा जाता है और उसका एक फोकस परवलयज के ही फोकस पर पड़ता है। उसका दूसरा फोकस परवलयज के निकट ही पड़ता है। इस व्यवस्था में परवलयज द्वारा निर्मित प्राथमिक बिंब से दीर्घवृत्तजीय, एक द्वितीयक बिंब काफी दूर बनता है।
सन्दर्भ
इन्हें भी देखें
- समतल दर्पण
- लेंस
- परवलयज परावर्तक (paraboloid reflector)
बाहरी कड़ियाँ
- [१] Java Applet to explore ray tracing.
- [२] Java applets to explore ray tracing for curved mirrors.
- Concave mirrors — real images Molecular Expressions Optical Microscopy Primer.
- Spherical mirrors Online physics lab.
- "Grinding the World's Largest Mirror" Popular Science, December 1935
| दर्पण | |
|---|---|
| समतल दर्पण | उत्तल दर्पण | अवतल दर्पण | |


