लाप्लास रूपान्तर

मुक्त ज्ञानकोश विकिपीडिया से
नेविगेशन पर जाएँ खोज पर जाएँ
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
टाइम डोमेन और फ्रेक्वेन्सी डोमेन

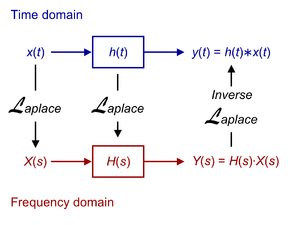
लाप्लास रूपान्तर (Laplace transform) एक प्रकार का समाकल रूपान्तर (integral transform) है। यह भौतिकी एवं इंजीनियरी के अनेकानेक क्षेत्रों में प्रयोग किया जाता है। उदाहरण के लिए परिपथ विश्लेषण में। इसको <math> \displaystyle\mathcal{L} \left\{f(t)\right\}</math> से निरूपित करते हैं। यह एक रैखिक संक्रिया है जो वास्तविक अर्गुमेन्ट t (t ≥ 0) वाले फलन f(t) को समिश्र अर्गुमेन्ट वाले फलन F(s) में बदल देता है।

लाप्लास रूपान्तर, प्रसिद्ध गणितज्ञ खगोलविद पिएर सिमों लाप्लास के नाम पर रखा गया है। लाप्लास रूपान्तर का उपयोग अवकल समीकरण तथा समाकल समीकरण (इंटीग्रल इक्वेशन) हल करने में किया जाता है।

परिभाषा

<math>F(s)
= \mathcal{L} \left\{f(t)\right\}
=\int_{0}^\infty e^{-st} f(t)\,dt.</math>

अनुबन्ध यह है कि उपरोक्त समाकलन का अस्तित्व हो। उपरोक्त प्रकार से परिभाषित लाप्लास रूपान्तर 'एकपक्षीय लाप्लास रूपान्तर' कहलाता है। लाप्लास रूपान्तर का द्विपक्षीय रूपान्तर निम्नलिखित प्रकार से पारिभाषित किया जाता है-

<math>F_B(s)
= \mathcal{L}\left\{f(t)\right\}
=\int_{-\infty}^{\infty} e^{-st} f(t)\,dt.</math>

गुण

रैखिकता

<math>\mathcal{L}\left\{a f(t) + b g(t) \right\}
 = a \mathcal{L}\left\{ f(t) \right\} +
   b \mathcal{L}\left\{ g(t) \right\}</math>

अवकलन

<math>\mathcal{L}\{f'(t)\}
 = s \mathcal{L}\{f(t)\} - f(0)</math>
<math>\mathcal{L}\{f(t)\}
 = s^2 \mathcal{L}\{f(t)\} - s f(0) - f'(0)</math>
<math> \mathcal{L}\left\{ f^{(n)}(t) \right\} = s^n \mathcal{L}\{f(t)\} - s^{n - 1} f(0) - \dots - f^{(n - 1)}(0) </math> <math> = s^n \mathcal{L}\{f(t)\} - \sum_{i=1}^{n} s^{n - i} f^{(i - 1)}(0) </math>

समाकलन

<math>\mathcal{L}\left\{ \int_{0^{-}}^{t}f(\tau )d\tau \right\} = {1 \over s} \mathcal{L}\{f\}</math>

द्वैत

<math>\mathcal{L}\{ t f(t)\}
 = -F'(s)</math>

आवृत्ति विस्थापन

<math>\mathcal{L}\left\{ e^{at} f(t) \right\} =
 F(s-a)</math>

समय विस्थापन

<math>\mathcal{L}\left\{ f(t - a) u(t - a) \right\}
 = e^{-as} F(s)</math>
<math>\mathcal{L}^{-1} \left\{ e^{-as} F(s) \right\}
 = f(t - a) u(t - a)</math>

टिप्पणी: <math>u(t)</math> का अर्थ है यूनिट स्टेप फलन

समय के n-घात से गुणा

<math>\mathcal{L}\{\,t^nf(t)\} = (-1)^nD_s^n[F(s)]</math>

संवलन (कॉन्वोलुशन)

<math>\mathcal{L}\{f*g\}
 = F(s)G(s)</math>

p आवर्तकाल वाले एक आवर्ती फलन का लाप्लास रूपान्तर

<math>\mathcal{L}\{ f \} = {1 \over 1 - e^{-ps}} \int_0^p e^{-st} f(t)\,dt</math>

प्रारम्भिक मान प्रमेय

<math>f(0^{+})=\lim_{s\to\infty}{sF(s)}</math>

अन्तिम मान प्रमेय

<math>f(\infty)=\lim_{s\to0}{sF(s)}</math>

प्रमुख फलनों के लाप्लास रूपान्तर

फलन समय डोमेन
<math>f(t) = \mathcal{L}^{-1} \left\{ F(s) \right\}</math> 		लाप्लास s-डोमेन
<math>F(s) = \mathcal{L}\left\{ f(t) \right\}</math> 		अभिसरण क्षेत्र (Region of convergence) सन्दर्भ
यूनिट इम्पल्स <math> \delta(t) \ </math> <math> 1 </math> <math> \mathrm{all} \ s \,</math> inspection
delayed impulse <math> \delta(t-\tau) \ </math> <math> e^{-\tau s} \ </math> time shift of
unit impulse
unit step <math> u(t) \ </math> <math> { 1 \over s } </math> Re(s) > 0 integrate unit impulse
delayed unit step <math> u(t-\tau) \ </math> <math> { e^{-\tau s} \over s } </math> Re(s) > 0 time shift of
unit step
ramp <math> t \cdot u(t)\ </math> <math>\frac{1}{s^2}</math> Re(s) > 0 integrate unit
impulse twice
nth power
(for integer n) 		<math> t^n \cdot u(t) </math> <math> { n! \over s^{n+1} } </math> Re(s) > 0
(n > −1) 		Integrate unit
step n times
qth power
(for complex q) 		<math> t^q \cdot u(t) </math> <math> { \Gamma(q+1) \over s^{q+1} } </math> Re(s) > 0
Re(q) > −1 		[१][२]
nth root <math> \sqrt[n]{t} \cdot u(t) </math> <math> { \Gamma(\frac{1}{n}+1) \over s^{\frac{1}{n}+1} } </math> Re(s) > 0 Set q = 1/n above.
nth power with frequency shift <math>t^{n} e^{-\alpha t} \cdot u(t) </math> <math>\frac{n!}{(s+\alpha)^{n+1}}</math> Re(s) > −α Integrate unit step,
apply frequency shift
delayed nth power
with frequency shift 		<math>(t-\tau)^n e^{-\alpha (t-\tau)} \cdot u(t-\tau) </math> <math> \frac{n! \cdot e^{-\tau s}}{(s+\alpha)^{n+1}} </math> Re(s) > −α Integrate unit step,
apply frequency shift,
apply time shift
exponential decay <math> e^{-\alpha t} \cdot u(t) \ </math> <math> { 1 \over s+\alpha } </math> Re(s) > −α Frequency shift of
unit step
two-sided exponential decay <math> e^{-\alpha|t|} \ </math> <math> { 2\alpha \over \alpha^2 - s^2 } </math> −α < Re(s) < α Frequency shift of
unit step
exponential approach <math>(1-e^{-\alpha t}) \cdot u(t) \ </math> <math>\frac{\alpha}{s(s+\alpha)} </math> Re(s) > 0 Unit step minus
exponential decay
sine <math> \sin(\omega t) \cdot u(t) \ </math> <math> { \omega \over s^2 + \omega^2 } </math> Re(s) > 0 Bracewell 1978, पृष्ठ 227
cosine <math> \cos(\omega t) \cdot u(t) \ </math> <math> { s \over s^2 + \omega^2 } </math> Re(s) > 0 Bracewell 1978, पृष्ठ 227
hyperbolic sine <math> \sinh(\alpha t) \cdot u(t) \ </math> <math> { \alpha \over s^2 - \alpha^2 } </math> Re(s) > |α| Williams 1973, पृष्ठ 88
hyperbolic cosine <math> \cosh(\alpha t) \cdot u(t) \ </math> <math> { s \over s^2 - \alpha^2 } </math> Re(s) > |α| Williams 1973, पृष्ठ 88
exponentially decaying
sine wave 		<math>e^{-\alpha t} \sin(\omega t) \cdot u(t) \ </math> <math> { \omega \over (s+\alpha)^2 + \omega^2 } </math> Re(s) > −α Bracewell 1978, पृष्ठ 227
exponentially decaying
cosine wave 		<math>e^{-\alpha t} \cos(\omega t) \cdot u(t) \ </math> <math> { s+\alpha \over (s+\alpha)^2 + \omega^2 } </math> Re(s) > −α Bracewell 1978, पृष्ठ 227
natural logarithm <math> \ln (t) \cdot u(t) </math> <math> - { 1 \over s}\, \left[ \ln(s)+\gamma \right] </math> Re(s) > 0 Williams 1973, पृष्ठ 88
Bessel function
of the first kind,
of order n 		<math> J_n(\omega t) \cdot u(t)</math> <math>\frac{ \left(\sqrt{s^2+ \omega^2}-s\right)^{n}}{\omega^n \sqrt{s^2 + \omega^2}}</math> Re(s) > 0
(n > −1) 		Williams 1973, पृष्ठ 89
Error function <math> \mathrm{erf}(t) \cdot u(t) </math> <math> {e^{s^2/4} \left(1 - \operatorname{erf} \left(s/2\right)\right) \over s}</math> Re(s) > 0 Williams 1973, पृष्ठ 89
Explanatory notes:

साँचा:col-begin साँचा:col-break

साँचा:col-break

  • t, एक वास्तविक संख्या है जो मोटे तौर पर "समय" को निरूपित करती है
    किन्तु t कोई भी स्वतंत्र राशि हो सकती है।
  • s is the complex angular frequency, and Re(s) is its real part.
  • α, β, τ, and ω are real numbers.
  • n is an integer.

साँचा:col-end


प्रतिलोम लाप्लास रूपान्तर

प्रतिलोम लाप्लास रूपान्तर (inverse Laplace transform) नीचे दिए गए समिश्र समाकल द्वारा निकाला जा सकता है। इस समाकल के कई नाम हैं, जैसे ब्रोमविच समाकल (Bromwich integra), फुर्ये-मेलिन समाकल (Fourier–Mellin integral) या मेलिन का प्रतिलोम सुत्र (Mellin's inverse formula):

<math>f(t) = \mathcal{L}^{-1}\{F\}(t) = \frac{1}{2 \pi i} \lim_{T\to\infty}\int_{\gamma - i T}^{\gamma + i T} e^{st} F(s)\, ds,</math>

जहाँ साँचा:math एक वास्तविक संख्या है ताकि समाकल का कन्टूर-पथ कन्वर्जेन्स के क्षेत्र साँचा:math के अन्दर हो। प्रतिलोम लाप्लास रूपान्तर निकालने का एक दूसरा सूत्र पोस्ट का प्रतिलोम सूत्र (Post's inversion formula) है।

उपयोग

उदाहरण १: किसी अवकल समीकरण का हल निकालना

नाभिकीय भौतिकी में जरेडियोसक्रिय क्षय को अभिव्यक्त करने वाला अवकल समीकरण नीचे दिया गया है। किसी नमूने में रेडियोसक्रिय परमाणुओं की संख्या साँचा:math है तथा इसके क्षय की दर साँचा:math के समानुपाती होती है। इसी को निम्नलिखित अवकल समीकरण द्वारा अभिव्यक्त किया जा सकता है-

<math>\frac{dN}{dt} = -\lambda N,</math>

जहाँ साँचा:math, क्षय नियतांक (decay constant) है। इस समीकरण का हल लाप्लास रूपान्तर की सहायता से निकाला जा सकता है।

इस समीकरण को एक ही पक्ष (side) में ले जाकर लिखने पर,

<math>\frac{dN}{dt} + \lambda N = 0.</math>

अब हम इस समीकरण के दोनों पक्षों का लाप्लास रूपान्तर लेते हैं।

<math>\left( s \tilde{N}(s) - N_0 \right) + \lambda \tilde{N}(s) = 0,</math>

जहाँ

<math>\tilde{N}(s) = \mathcal{L}\{N(t)\}</math>

तथा

<math>N_0 = N(0).</math>

इसका हल करने पर,

<math>\tilde{N}(s) = \frac{N_0}{s + \lambda}.</math>

अन्त में हम प्रतिलोम लाप्लास रूपान्तर लेते हें जिससे सामान्य हल प्राप्त होता है।

<math>\begin{align}
 N(t) &= \mathcal{L}^{-1} \{\tilde{N}(s)\} = \mathcal{L}^{-1}\! \left\{ \frac{N_0}{s + \lambda} \right\}\\
      &= \ N_0 e^{-\lambda t},

\end{align}</math>

s-डोमेन में तुल्य परिपथ और प्रतिबाधाएँ

क्षणिक परिपथों के विश्लेषण में प्रायः लाप्लास रूपान्तर का उपयोग किया जाता है। इसके लिए परिपथ के अवयवों को साँचा:math-डोमेन में बदलकर काम को आगे बढ़ाते हैं। नीचे तुल्य परिपथ दिए गये हैं-

साँचा:math-domain equivalent circuits

अनुप्रयोग : दो लूप वाले एक परिपथ की क्षणिक अनुक्रिया (रिस्पॉन्स)

दो लूप वाला एक परिपथ

पार्श्व चित्र को देखें जिसमें दो लूप हैं। इनमें बहने वाली धारा <math>i_1</math> तथा <math>i_2</math> चित्र में दर्शायी गयी हैं। माना <math>i_1</math> तथा <math>i_2</math> के आरम्भिक मान शून्य हैं, अर्थात् <math>i_1(0)=0</math> और <math>i_2(0)=0</math>। किरखॉफ के नियम के अनुसार,

<math>{di_1(t) \over dt}+5i_1(t)+40i(t)=110</math> (1)

<math>2{di_2(t) \over dt}+10i_2(t)+40i(t)=110</math> (2)

चित्र से स्पष्ट है कि <math>i(t)=i_1(t)+i_2(t)</math>,

<math>{di_1(t) \over dt}+45i_1(t)+40i_2(t)=110</math>

<math>{di_2(t) \over dt}+20i_2(t)+25i_2(t)=55</math> (समीकरण (2) को 2 से भाग देने पर)

इन पर लाप्लास रूपान्तर लगाने पर,

<math>sI_1(s)-i_1(0)+45I_1(s)+40I_2(s)=\frac{110}{s}</math>

<math>sI_2(s)-i_2(0)+20I_1(s)+25I_2(s)=\frac{55}{s}</math>

या,

<math>(s+45)I_1(s)+40I_2(s)=\frac{110}{s}</math>

<math>20I_1(s)+(s+25)I_2(s)=\frac{55}{s}</math>

या,

<math>\begin{bmatrix} (s+45) & 40 \\ 20 & (s+25) \end{bmatrix}\begin{bmatrix} I_1(s)\\ I_2(s) \end{bmatrix}=\begin{bmatrix} 110/s \\ 55/s\end{bmatrix}</math>

इसका हल निम्नलिखित है:

<math>\begin{bmatrix} I_1(s)\\ I_2(s)\end{bmatrix}=\frac{1}{(s+25)(s+45)-800}\begin{bmatrix} (s+25) & -40 \\ -20 & (s+45) \end{bmatrix}\begin{bmatrix} 110/s\\ 55/s\end{bmatrix}</math>

अतः,

<math>I_1(s)=\frac{1}{s^2+70s+325}\biggl(\frac{110}{s}(s+25)-\frac{2200}{s}\biggr)=\frac{1}{(s+5)(s+65)}\biggl(110+\frac{550}{s}\biggr)</math>

<math>I_2(s)=\frac{1}{s^2+70s+325}\biggl(-\frac{2200}{s}+\frac{55}{s}(s+45)\biggr)=\frac{1}{(s+5)(s+65)}\biggl(55+\frac{275}{s}\biggr)</math>

ध्यान दें कि <math>I_1(s)=2I_2(s)</math> अतः हम केवल <math>I_2(s)</math> की गणना ही करेंगे।

<math>I_2(s)=\frac{1}{(s+5)(s+65)}\biggl(\frac{55s+275}{s}\biggr)=\frac{55}{(s+5)(s+65)}\biggl(\frac{s+5}{s}\biggr)=\frac{55}{s(s+65)}</math>

इससे,

<math>i_2(t)=\frac{55}{65}(1-e^{-65t})=\frac{11}{13}(1-e^{-65t})</math>

चूंकि <math>i_1(t)=2i_2(t)</math>, अतः

<math>i_2(t)=\frac{22}{13}(1-e^{-65t})</math>

सन्दर्भ

  1. ↑ Mathematical Handbook of Formulas and Tables (3rd edition), S. Lipschutz, M.R. Spiegel, J. Liu, Schuam's Outline Series, p.183, 2009, ISBN 978-0-07-154855-7 - provides the case for real q.
  2. ↑ http://mathworld.wolfram.com/LaplaceTransform.html स्क्रिप्ट त्रुटि: "webarchive" ऐसा कोई मॉड्यूल नहीं है। - Wolfram Mathword provides case for complex q

इन्हें भी देखें

बाहरी कड़ियाँ

"https://hiwiki.iiit.ac.in/index.php?title=लाप्लास_रूपान्तर&oldid=139347" से लिया गया