लजान्द्र बहुपद
नेविगेशन पर जाएँ
खोज पर जाएँ
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
साँचा:asbox गणित में लजान्द्र बहुपद (Legendre Polynomial) वे बहुपद हैं जो लजान्द्र के अवकल समीकण के हल हैं:
- <math>{d \over dx} \left[ (1-x^2) {d \over dx} P_n(x) \right] + n(n+1)P_n(x) = 0.</math>
यह नामकरण आद्रियें मारि लजान्द्र के नाम पर किया गया है। ये बहुपद लांबिक फलन (आर्थोगोनल फलन) के सरलतम उदाहरण हैं।
कुछ लजान्द्र बहुपद
आरम्भ के ग्यारह लजान्द्र बहुपद नीचे दिए गए हैं:
| n | <math>P_n(x)\,</math> |
| 0 | <math>1\,</math> |
| 1 | <math>x\,</math> |
| 2 | <math>\begin{matrix}\frac12\end{matrix} (3x^2-1) \,</math> |
| 3 | <math>\begin{matrix}\frac12\end{matrix} (5x^3-3x) \,</math> |
| 4 | <math>\begin{matrix}\frac18\end{matrix} (35x^4-30x^2+3)\,</math> |
| 5 | <math>\begin{matrix}\frac18\end{matrix} (63x^5-70x^3+15x)\,</math> |
| 6 | <math>\begin{matrix}\frac1{16}\end{matrix} (231x^6-315x^4+105x^2-5)\,</math> |
| 7 | <math>\begin{matrix}\frac1{16}\end{matrix} (429x^7-693x^5+315x^3-35x)\,</math> |
| 8 | <math>\begin{matrix}\frac1{128}\end{matrix} (6435x^8-12012x^6+6930x^4-1260x^2+35)\,</math> |
| 9 | <math>\begin{matrix}\frac1{128}\end{matrix} (12155x^9-25740x^7+18018x^5-4620x^3+315x)\,</math> |
| 10 | <math>\begin{matrix}\frac1{256}\end{matrix} (46189x^{10}-109395x^8+90090x^6-30030x^4+3465x^2-63)\,</math> |
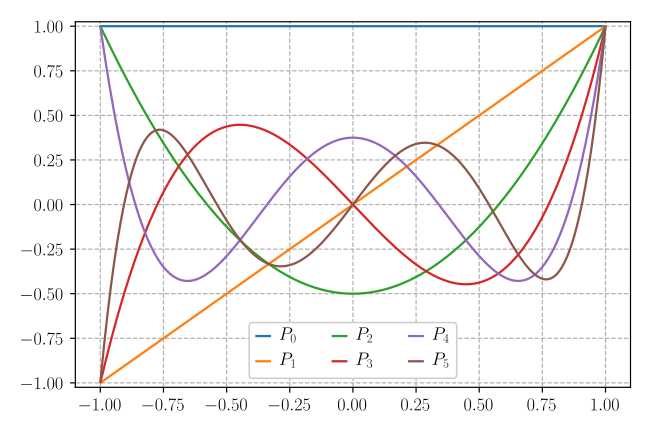
नीचे के चित्र में n=5 तक के लजान्द्र बहुपदों का आरेख (ग्राफ) दिखाया गया है।