फ़ूर्ये श्रेणी
गणित में फूर्ये श्रेणी (Fourier series) एक ऐसी अनन्त श्रेणी है जो f आवृत्ति वाले किसी आवर्ती फलन (periodic function) को f, 2f, 3f, आदि आवृत्तियों वाले ज्या और कोज्या फलनों के योग के रूप में प्रस्तुत करती है। इसका प्रयोगे सबसे पहले जोसेफ फ़ूर्ये (१७६८ - १८३०) ने धातु की प्लेटों में उष्मा प्रवाह एवं तापमान की गणना के लिये किया था। किन्तु बाद में इसका उपयोग अनेकानेक क्षेत्रों में हुआ और यह विश्लेषण का एक क्रान्तिकारी औजार साबित हुआ।
इसकी सहायता से कठिन से कठिन फलन भी ज्या और कोज्या फलनों के योग के रूप में प्रकट किये जाते हैं जिससे इनसे सम्बन्धित गणितीय विश्लेषण अत्यन्त सरल हो जाते हैं।
फुरिअर श्रेणी के उपयोग
- वैद्युत प्रौद्योगिकी में - विद्युत परिपथ में बहने वाली धारा और वोल्टता आदि की गणना में
- कम्पन के विश्लेषण में (यांत्रिक, ध्वनि या विद्युतचुम्बकीय कम्पन)
- संकेत प्रसंस्करण (signal processing) में
- छवि प्रसंस्करण (image processing) में
2π आवर्तकाल वाले आवर्ती फलनों के लिये फुरिअर श्रेणी
माना f(x), वास्तविक चर x का एक आवर्ती फलन है जिसका आवर्त काल 2π है अर्थात f(x+2π) = f(x) तो,
- <math>f(x) = \frac{a_0}{2} +\sum_{n=1}^{\infty}[a_n \cos(nx) + b_n \sin(nx)]</math>
इस श्रेणी को फुरिअर श्रेणी कहते हैं। <math>a_0,a_1,...</math> और <math>b_1, b_2, ...</math> को फुरिअर गुणांक कहा जाता है। ये गुणांक वास्तविक संख्या या समिश्र संख्या हो सकते हैं।
- <math>a_0= \frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x)dx,</math>
- <math>a_n= \frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x)\cos(nx)dx,</math>
- <math>b_n= \frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x)\sin(nx)dx,</math>
फुरिअर श्रेणी का एक सरल उदाहरण
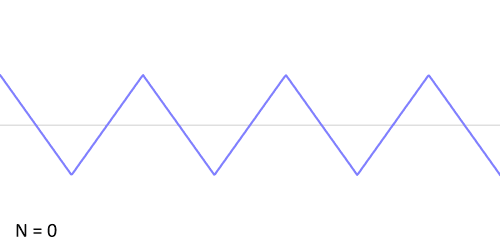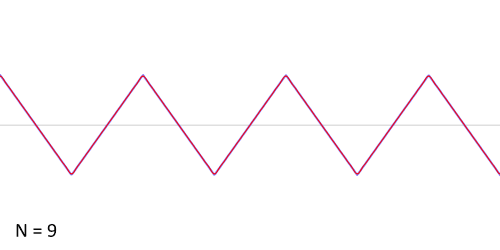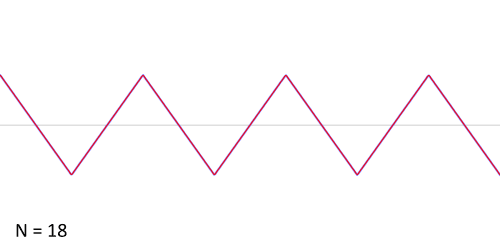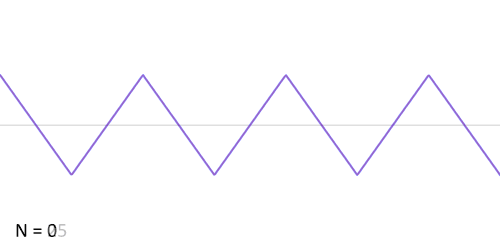
माना कि दिया हुआ फलन आरीदाँत फलन (sawtooth function) है जिसे निम्नवत गणितीय रूप से प्रकट कर सकते हैं:
- <math>f(x) = x, \quad \mathrm{for} \quad -\pi < x < \pi,</math>
- <math>f(x + 2\pi) = f(x), \quad \mathrm{for} \quad -\infty < x < \infty.</math>
इस फलन के लिये फुरिअर गुणांक इस प्रकार होंगे:
- <math>\begin{align}
a_n &{} = \frac{1}{\pi}\int_{-\pi}^{\pi}x \cos(nx)\,dx = 0. \\ b_n &{}= \frac{1}{\pi}\int_{-\pi}^{\pi} x \sin(nx)\, dx = 2\frac{(-1)^{n+1}}{n}.\end{align}</math>
अत:
- <math>
\begin{align} f(x) &= \frac{a_0}{2} + \sum_{n=1}^{\infty}\left[a_n\cos\left(nx\right)+b_n\sin\left(nx\right)\right] \\ &=2\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n} \sin(nx), \quad \mathrm{for} \quad -\infty < x < \infty . \;\;\; (*) \end{align} </math>
इन्हें भी देखें
- जोसेफ फ़ूर्ये
- फ़ूर्ये विश्लेषण
- फ़ूर्ये रूपान्तर (Fourier transform)
- मूल आवृत्ति
बाहरी कड़ियाँ
- Phasor Phactory Allows custom control of the harmonic amplitudes for arbitrary terms
- Java applet shows Fourier series expansion of an arbitrary function
- Example problems - Examples of computing Fourier Series
- Fourier series explanationसाँचा:category handlerसाँचा:main otherसाँचा:main other[dead link] - A simple, non-mathematical approach
- Fourier Series Module by John H. Mathews
- Joseph Fourier - A site on Fourier's life which was used for the historical section of this article