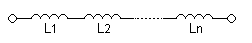प्रेरक
प्रेरक या इंडक्टर (inductor) यह एक passive component है जिस से होकर विद्युत धारा प्रवाहित कराया जाता है तो यह चुम्बकीय क्षेत्र के रूप में उर्जा का भंडारण करता है। प्रेरक द्वारा चुम्बकीय उर्जा के भंडारण की क्षमता को इसका प्रेरकत्व (inductance) कहा जाता है और इसे मापने की इकाई हेनरी है।
प्रेरक को साधारण भाषा में 'चोक' (choke) और 'कुण्डली' (coil) भी कहते हैं। इसका फुल वीडियो youtube STUDY IN XYZ CHAINNEL पर देख सकते हैं
उपयोग
- वैद्युत फिल्टर बनाने के लिये
- इम्पीडैंस मैचिंग के लिये
- ट्यूबलाइट आदि को जलाने के लिये आरम्भ में हजारों वोल्ट पैदा करने एवं जलने के बाद उससे बहने वाली धारा को सीमित रखने के लिये।
- पुरानी कारों एवं स्कूटरों आदि में स्पार्क पैदा करने के लिये (इग्नीशन क्वायल)
परिपथ में प्रेरकत्व
ऊर्जा
- प्रेरकत्व में भण्डारित ऊर्जा
- <math> E_\mathrm{induttore}= W = {1 \over 2} L I^2 </math>
जहाँ I प्रेरक से होकर प्रवाहित धारा और L प्रेरकत्व है।
धारा एवं वोल्टता में सम्बन्ध
- <math>v(t) = L \frac{di(t)}{dt}</math>
यदि प्रेरक से साइनवक्रीय I धारा बह रही हो तो, उसका वोल्टेज
- <math>V = I \times \omega L</math>
जहाँ ω का मान,
- <math> \omega = 2 \pi f</math>
जहाँ f प्रत्यावर्ती धारा की आवृत्ति है।
- <math>\mathbf X_L = \omega L = 2 \pi f L </math>
यहाँ XL को प्रेरकीय प्रतिबाधा (इंडक्टिव रिएक्टैन्स) कहते हैं।
प्रेरक में जब साइनाकारी विद्युत धारा बहती है तो उसकी धारा की कला, उसके सिरों के बीच विभवान्तर से ९० डिग्री पीछे होता है।
- <math>\mathbf Z = j \omega L = j 2 \pi f L </math>
- Jp yadav
प्रेरकों का संयोजन
प्रेरकों को समान्तर क्रम में या श्रेणीक्रम में जोड़ा जा सकता है।
समान्तर क्रम में जुड़े n प्रेरकों का तुल्य प्रेरकत्व Leq के लिये निम्नलिखित सम्बन्ध है-
- <math> \frac{1}{L_\mathrm{eq}} = \frac{1}{L_1} + \frac{1}{L_2} + \cdots + \frac{1}{L_n}</math>
यहाँ माना गया है कि किसी भी प्रेरक का किसी दूसरे के साथ अन्योन्य प्रेरकत्व (म्युचुअल इण्डक्टैस) शून्य है।
श्रेणीक्रम में जुड़े प्रेरकों का तुल्य प्रेरकत्व,
- <math> L_\mathrm{eq} = L_1 + L_2 + \cdots + L_n \,\! </math>
प्रेरकत्व गणना के लिये सूत्र
| संरचना | सूत्र | प्रतीकों के अर्थ | टिप्पणी |
|---|---|---|---|
| बेलनाकार वायु-कोर प्रेरक[१] | <math>L=\frac{\mu_0KN^2A}{l}</math> |
|
|
| Straight wire conductor[२] | <math>L = \frac{\mu_{0}}{2\pi}\left[l\ln\frac{l+\sqrt{l^{2}+c^{2}}}{c}-\sqrt{l^{2}+c^{2}} + c \right]</math>
|
|
exact if ω = 0 or ω = ∞ |
| <math>L = 0.2 l\left(\ln\frac{4l}{d}-1\right)</math> -0+3% |
|
| |
| <math>L = 0.2 l\left(\ln\frac{4l}{d}-\frac{3}{4}\right)</math> +0-3% |
|
| |
| वायु-क्रोड लघु बेलनाकार कुण्डली[३] | <math>L=\frac{r^2N^2}{9r+10l}</math> |
| |
| Multilayer air-core coilसाँचा:category handler[<span title="स्क्रिप्ट त्रुटि: "string" ऐसा कोई मॉड्यूल नहीं है।">citation needed] | <math>L = \frac{0.8r^2N^2}{6r+9l+10d}</math> |
| |
| Flat spiral air-core coilसाँचा:category handler[<span title="स्क्रिप्ट त्रुटि: "string" ऐसा कोई मॉड्यूल नहीं है।">citation needed] | <math>L=\frac{r^2N^2}{(20r+28d)}</math> |
| |
| <math>L=\frac{r^2N^2}{8r+11d}</math> |
| ||
| Toroidal core (circular cross-section)साँचा:category handler[<span title="स्क्रिप्ट त्रुटि: "string" ऐसा कोई मॉड्यूल नहीं है।">citation needed] | <math>L=\mu_0\mu_r\frac{r^2N^2}{D}</math> |
|
सन्दर्भ
इन्हें भी देखें
बाहरी कड़ियाँ
- How stuff works The initial concept, made very simple
- Capacitance and Inductance - A chapter from an online textbook
- Spiral inductor models. Article on inductor characteristics and modeling.
- Online coil inductance calculator. Online calculator calculates the inductance of conventional and toroidal coils using formulas 3, 4, 5, and 6, above.
- AC circuits
- Understanding coils and transforms
- ↑ अ आ साँचा:cite journal
- ↑ स्क्रिप्ट त्रुटि: "citation/CS1" ऐसा कोई मॉड्यूल नहीं है।
- ↑ ARRL Handbook, 66th Ed. American Radio Relay League (1989).