थेवेनिन का प्रमेय
थेवेनिन का प्रमेय, परिपथ सिद्धान्त का एक महत्वपूर्ण प्रमेय है। इसे फ्रांस के टेलेग्राफ इंजीनीयर लियों चार्ल्स थेवेनिन (Léon Charles Thévenin (1857–1926)) ने प्रतिपादित किया था।
इसके अनुसार, वोल्टता स्रोत, धारा स्रोत एवं प्रतिरोधकों से निर्मित किसी भी रैखिक परिपथ का इसके किन्हीं दो सिरों (टर्मिनल्स) के बीच व्यवहार एक तुल्य वोल्तता स्रोत Vth एवं तुल्य प्रतिरोधक Rth के श्रेणीक्रम के द्वारा निरूपित किया जा सकता है। यह केवल रैखिक डीसी परिपथ में ही लागू नहीं होता बल्कि किसी एकल आवृत्ति वाले प्रत्यावर्ती धारा के स्रोत एवं सामान्यीकृत प्रतिबाधा से युक्त परिपथों के लिये भी लागू होता है। इस सिद्धान्त की खोज सबसे पहले जर्मनी के वैज्ञानिक हर्मन वॉन हेल्मोल्ट्ज (Hermann von Helmholtz) ने सन् १८५३ में की थी[१], किन्तु बाद में थेवेनिन ने सन् १८८३ में इसे 'पुन: खोजा'।[२][३]
उदाहरण
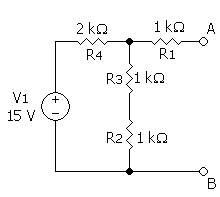
- तुल्य वोल्तता की गणना (calculating the equivalent voltage)
- <math>
V_\mathrm{eq} = {R_2 + R_3 \over (R_2 + R_3) + R_4} \cdot V_\mathrm{1} </math>
- <math>
= {1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega \over (1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega) + 2\,\mathrm{k}\Omega} \cdot 15 \,\mathrm{V} </math>
- <math>
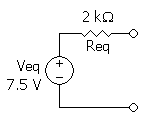
= {1 \over 2} \cdot 15 \, \mathrm{V} = 7.5 \,\mathrm{V} </math> (notice that R1 is not taken into consideration, as above calculations are done in an open circuit condition between A and B, therefore no current flows through this part which means there is no current through R1 and therefore no voltage drop along this part)
- तुल्य प्रतिरोध की गणना (Calculating equivalent resistance)
- <math>
R_\mathrm{eq} = R_1 + \left [ \left (R_2 + R_3 \right) \| R_4 \right) ] </math>
- <math>
= 1\,\mathrm{k}\Omega + \left [ \left (1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega \right) \| 2\,\mathrm{k}\Omega \right) ] </math>
- <math>
= 1\,\mathrm{k}\Omega + \left({1 \over (1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega)} + {1\over (2\,\mathrm{k}\Omega) }\right)^{-1} = 2\,\mathrm{k}\Omega </math>
नॉर्टन तुल्य में परिवर्तन
किन्हीं दो आसंधि (नोड) के बीच, किसी रैखिक परिपथ को नॉर्टन तुल्य परिपथ के रूप में भी निरूपित किया जा सकता है। नॉर्टन तुल्य परिपथ एक धारा स्रोत और उसके समानन्तर जुड़ा एक प्रतिरोध होता है। थेवनिन तुल्य परिपथ तथा नॉर्टन तुल्य परिपथ के अवयवों के मान के बीच निम्नलिखित सम्बन्ध होता है-
- <math>R_{Th} = R_{No} \!</math>
- <math>V_{Th} = I_{No} R_{No} \!</math>
- <math>V_{Th} / R_{Th} = I_{No}\!</math>
व्यावहारिक सीमाएँ
- यह केवल रैखिक परिपथों के लिए लागू होता है, अरैखिक परिपथ के लिए नहीं। बहुत से परिपथ, स्रोतों की वोल्टता या धारा की किसी एक सीमा के भीतर ही रैखिक परिपथ जैसा व्यवहार करते हैं, अतः थेवनिन तुल्य भी केवल उस रैखिक सीमा के लिए वैध होता है, सीमा के बाहर नहीं।
- चूंकि शक्ति, वोल्टता या धारा के साथ रैखिक रूप से नहीं बदलती (P=V2/R) अतः थेवनिन तुल्य परिपथ में होने वाला शक्ति-क्षय, मूल परिपथ के अवयवों में होने वाले कुल शक्ति-क्षय से अलग होता है। अर्थात थेवनिन तुल्य परिपथ, शक्ति क्षय की दृष्टि से 'तुल्य' नहीं होता।
टिपणी
- ↑ H. Helmholtz (1853) "Über einige Gesetze der Vertheilung elektrischer Ströme in körperlichen Leitern mit Anwendung auf die thierisch-elektrischen Versuche" [Some laws concerning the distribution of electrical currents in conductors with applications to experiments on animal electricity], Annalen der Physik und Chemie, vol. 89, no. 6, pages 211–233, available online http://gallica.bnf.fr/ark:/12148/bpt6k151746.image.f225.langFR स्क्रिप्ट त्रुटि: "webarchive" ऐसा कोई मॉड्यूल नहीं है।
- ↑ L. Thévenin (1883) "Extension de la loi d’Ohm aux circuits électromoteurs complexes" [Extension of Ohm’s law to complex electromotive circuits], Annales Télégraphiques (Troisieme série), vol. 10, pages 222–224. Reprinted as: L. Thévenin (1883) "Sur un nouveau théorème d’électricité dynamique" [On a new theorem of dynamic electricity], Comptes Rendus hebdomadaires des séances de l’Académie des Sciences, vol. 97, pages 159–161.
- ↑ Don H. Johnson (April 2003) "Equivalent circuit concept: the voltage-source equivalent," Proceedings of the IEEE, vol. 91, no. 4, pages 636-640. Available on-line at: http://www.ece.rice.edu/~dhj/paper1.pdf स्क्रिप्ट त्रुटि: "webarchive" ऐसा कोई मॉड्यूल नहीं है। .
इन्हें भी देखें
- नॉर्टन का प्रमेय (Norton's theorem)
- विद्युत प्रतिबाधा (Electrical impedance)
- अध्यारोपण प्रमेय (Superposition theorem)
- Extra element theorem
- Nodal analysis
- Mesh analysis
- स्टार-डेल्टा परिवर्तन (Y-Δ transform या Star-Delta transformation)
- Source transformation
- Léon Charles Thévenin
- Edward Lawry Norton
बाहरी कड़ियाँ
- Origins of the equivalent circuit concept
- Thevenin's theorem at allaboutcircuits.com
- ECE 209: Review of Circuits as LTI Systems — At end, shows application of Thévenin's theorem that turns complicated circuit into a simple first-order low-pass filter voltage divider with obvious time constant and gain.