नॉर्टन का प्रमेय

नॉर्टन का प्रमेय (Norton's theorem) परिपथ विश्लेषण से सम्बन्धित एक प्रमेय है, जिसके अनुसार
- किसी रैखिक विद्युत परिपथ में यदि केवल वोल्टता स्रोत, धारा स्रोत और प्रतिरोध हों तो इसके सिरों A–B के बीच इसे इसके तुल्य वैशिष्ट्य वाले परिपथ के रूप में अभिव्यक्त किया जा सकता है जिसमें केवल एक धारा स्रोत Ino एक प्रतिरोधक Rno के समान्तर क्रम में जुड़ा होगा।
- इस धारा स्रोत Ino का मान A-B सिरों को 'शॉर्ट' करने पर उस शॉर्ट से होकर बहने वाली धारा के बराबर होता है।
- उपरोक्त तुल्य प्रतिरोध Rno का मान सभी वोल्टता स्रोतों को शॉर्ट करने एवं सभी धारा स्रोतों को ओपेन करने के बाद सिरों A-B के बीच प्राप्त तुल्य प्रतिरोध के बराबर होगा।
यह प्रमेय प्रत्यावर्ती धारा के लिए भी लागू किया जा सकता है।
नॉर्टन का प्रमेय एवं इसका द्वैत, थेवेनिन का प्रमेय (Thévenin's theorem) परिपथ विश्लेषण में बहुतायत में प्रयुक्त होते हैं। नॉर्टन के प्रमेय की उपपत्ति सन १९२६ में एक साथ स्वतन्त्र रूप से सिमेन्स और हैक्से (Siemens & Halske) तथा बेल प्रयोगशाला के इंजीनियर एडवर्ड लारी नॉर्टन (Edward Lawry Norton) ने किया था।
उदाहरण
 |
 |
 |

|
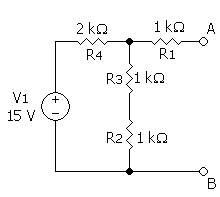
ऊपर के चित्र में, R4 से बहने वाली धारा, Itotal की गणना :
- <math>
I_\mathrm{total} = {15 \mathrm{V} \over 2\,\mathrm{k}\Omega + (1\,\mathrm{k}\Omega \| (1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega))} = 5,625 \mathrm{mA} </math>
अब A और B के बीच बने 'शॉर्ट' से होकर बहने वाली धारा की गणना कर सकते हैं (Itotal का दो धाराओं में विभाजन के सूत्र से) :
- <math>
I = {1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega \over (1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega)} \cdot I_\mathrm{total} </math>
- <math>
= 2/3 \cdot 5.625 \mathrm{mA} = 3.75 \mathrm{mA} </math>
अब A और B के बीच तुल्य प्रतिरोध की गणना करते हैं (V1 को शॉर्ट करके):
- <math>
R = 1\,\mathrm{k}\Omega +( 2\,\mathrm{k}\Omega \| (1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega)) = 2\,\mathrm{k}\Omega </math>
इस प्रकार हमे नॉर्टन तुल्य परिपथ के लिए आवशयक दोनों प्राचल (पैरामीटर) मिल गए हैं। सबसे दाहिने वाले चित्र नॉर्टन तुल्य परिपथ है जिसमें 2 kΩ का एक प्रतिरोध 3.75mA के एक धारा स्रोत के समान्तर जुड़ा हुआ है।
उदाहरण-२
नॉर्टन और थेवनिन परिपथों का परस्पर परिवर्तन
निम्नलिखित सूत्रों का उपयोग करते हुए हम नॉर्टन परिपथ को थेवनिन परिपथ में या थेवनिन परिपथ को नॉर्टन परिपथ में बदल सकते हैं-
- नॉर्टन से थेवनिन :
- <math>V_{Th} = I_{N} \times R_{N}</math>
- <math>R_{Th} = R_{N}</math>
- थेवनिन से नॉर्टन :
- <math>I_{N} = V_{Th} \div R_{Th}</math>
- <math>R_{N} = R_{Th}</math>
सन्दर्भ
इन्हें भी देखें
- थेवेनिन का प्रमेय (Thévenin's theorem)
- परिपथ विश्लेषण

