जड़त्वाघूर्णों की सूची
नेविगेशन पर जाएँ
खोज पर जाएँ
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
यहाँ पर विभिन्न आकार-प्रकार के पिण्डों के जड़त्वाघूर्ण दिये गये हैं। ज। दत्वाघूर्ण की इकाई की विमा द्रव्यमान × लम्बाई2 होती है। नीचे दिये गये व्यंजकों की गणना में यह माना गया है कि घनत्व सर्वत्र समान है।
टिप्पणी: जहाँ कहीं भी अलग से न कहा गया हो, यह माना गया है कि घूर्णन-अक्ष द्रव्यमान केन्द्र से जाता है।
| वर्णन | चित्र | जड़त्वाघूर्ण | टिप्पणी |
|---|---|---|---|
| पतला बेलनाकार शेल (shell) जिसके सिरे खुले हैं, त्रिज्या r तथा द्रव्यमान m |  |
<math>I = m r^2 \,\!</math> | शेल की मोटाई को नगण्य (शून्य) माना गया है। यह अगले पिण्ड का एक विशेष दशा है जिसमें r1=r2. |
| मोटी दिवार वाली खुले सिरों वाली बेलनाकार नली जिसकी अन्त:त्रिज्या r1, वाह्य त्रिज्या r2, लम्बाई h एवं द्रव्यमान m | 
|
<math>I_z = \frac{1}{2} m\left({r_1}^2 + {r_2}^2\right)</math>[१] <math>I_x = I_y = \frac{1}{12} m\left[3\left({r_2}^2 + {r_1}^2\right)+h^2\right]</math> or when defining the normalized thickness tn = t/r and letting r = r2, then <math>I_z = mr^2\left(1-t_n+\frac{1}{2}t_n^2\right) </math> |
घनत्व ρ और उपरोक्त ज्यामिति के साथ <math>I_z = \frac{1}{2} \pi\rho h\left({r_2}^4 - {r_1}^4\right)</math> |
| r त्रिज्या, h उंचाई, तथा m द्रव्यमान का ठोस बेलन |  |
<math>I_z = \frac{m r^2}{2}\,\!</math> <math>I_x = I_y = \frac{1}{12} m\left(3r^2+h^2\right)</math> |
This is a special case of the previous object for r1=0. |
| Thin, solid disk of radius r and mass m |  |
<math>I_z = \frac{m r^2}{2}\,\!</math> <math>I_x = I_y = \frac{m r^2}{4}\,\!</math> |
This is a special case of the previous object for h=0. |
| Thin circular hoop of radius r and mass m |  |
<math>I_z = m r^2\!</math> <math>I_x = I_y = \frac{m r^2}{2}\,\!</math> |
This is a special case of a torus for b=0. (See below.) |
| Solid sphere of radius r and mass m |  |
<math>I = \frac{2 m r^2}{5}\,\!</math> | A sphere can be taken to be made up of a stack of infinitesimal thin, solid discs, where the radius differs from 0 to r. |
| Hollow sphere of radius r and mass m |  |
<math>I = \frac{2 m r^2}{3}\,\!</math> | Similar to the solid sphere, only this time considering a stack of infinitesimal thin, circular hoops. |
| Oblate Spheroid of major a, minor b and mass m | <math>I = \frac{2 m b^2}{3}\,\!</math> | — | |
| Right circular cone with radius r, height h and mass m |  |
<math>I_z = \frac{3}{10}mr^2 \,\!</math> <math>I_x = I_y = \frac{3}{5}m\left(\frac{r^2}{4}+h^2\right) \,\!</math> |
— |
| Solid cuboid of height h, width w, and depth d, and mass m |  |
<math>I_h = \frac{1}{12} m\left(w^2+d^2\right)</math> <math>I_w = \frac{1}{12} m\left(h^2+d^2\right)</math> <math>I_d = \frac{1}{12} m\left(h^2+w^2\right)</math> |
For a similarly oriented cube with sides of length <math>s</math>, <math>I_{CM} = \frac{m s^2}{6}\,\!</math>. |
| Thin rectangular plane of height h and of width w and mass m |  |
<math>
I_c = \frac {m(h^2 + w^2)}{12}\,\!</math>||— | |
| Thin rectangular plane of height h and of width w and mass m (Axis of rotation at the end of the plate) |
 |
<math>I_e = \frac {m h^2}{3}+\frac {m w^2}{12}\,\!</math> | — |
| Rod of length L and mass m |  |
<math>I_{\mathrm{center}} = \frac{m L^2}{12} \,\!</math> | This expression assumes that the rod is an infinitely thin (but rigid) wire. This is a special case of the previous object for w=L and h=d=0. |
| Rod of length L and mass m (Axis of rotation at the end of the rod) |
 |
<math>I_{\mathrm{end}} = \frac{m L^2}{3} \,\!</math> | This expression assumes that the rod is an infinitely thin (but rigid) wire. |
| Torus of tube radius a, cross-sectional radius b and mass m. | 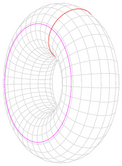 |
About a diameter: <math>\frac{1}{8}\left(4a^2 + 5b^2\right)m</math> About the vertical axis: <math>\left(a^2 + \frac{3}{4}b^2\right)m</math> |
— |
| Plane polygon with vertices <math>\vec{P}_{1}</math>, <math>\vec{P}_{2}</math>, <math>\vec{P}_{3}</math>, ..., <math>\vec{P}_{N}</math> and mass <math>m</math> uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through the origin. |  |
\vec{P}_{n+1}\times\vec{P}_{n}\|(\vec{P}^{2}_{n+1}+\vec{P}_{n+1}\cdot\vec{P}_{n}+\vec{P}_{n}^{2})}{\sum\limits_{n=1}^{N}\|\vec{P}_{n+1}\times\vec{P}_{n}\|}</math> | — |
इन्हें भी देखें
- समान्तर अक्ष का प्रमेय (Parallel axis theorem)
- क्षेत्राघूर्णों की सूची (List of area moments of inertia)
- जड़त्वाघूर्ण टेंसरों की सूची (List of moment of inertia tensors)
सन्दर्भ
- ↑ Classical Mechanics - Moment of inertia of a uniform hollow cylinder स्क्रिप्ट त्रुटि: "webarchive" ऐसा कोई मॉड्यूल नहीं है।. LivePhysics.com. Retrieved on 2008-01-31.