उत्सर्जन सिद्धांत
उत्सर्जन सिद्धांत (साँचा:lang-en) को विशिष्ट आपेक्षिकता सिद्धांत का प्रतिस्पर्ध्दा सिद्धांत भी कहा जाता है, क्योंकि यह सिद्धांत भी माइकलसन मोर्ले प्रयोग के परिणामों को समझाने में सक्षम रहा था। उत्सर्जन सिद्धांत प्रकाश संचरण के लिए कोई प्रधान निर्देश तंत्र नहीं होने के कारण आपेक्षिकता सिद्धांत का पालन करते हैं, लेकिन ये सिद्धांत निश्चरता अभिगृहीत के स्थान पर स्रोत के सापेक्ष उत्सर्जित प्रकाश का प्रकाश के वेग c लेते हैं। अतः उत्सर्जन सिद्धांत सरल न्यूटनीय सिद्धांत के साथ विद्युतगतिकी और यांत्रिकी को जोड़ती है। यद्दपि यहाँ वैज्ञानिक मुख्यधारा के बाहर इस सिद्धांत के समर्थक अब तक भी हैं, यह सिद्धांत अधिकांश वैज्ञानिकों द्वारा अन्त में उपयोग रहित माना जाता है।[१][२]
इतिहास
उत्सर्जन सिद्धांतो से सबसे अधिक नाम आइज़क न्यूटन का नाम जोड़ा जाता है।
उत्सर्जन सिद्धांत के खण्डन
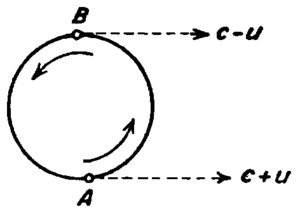
उत्सर्जन सिद्धांतों को परखने के लिए यह व्यवस्था डी सिटर (de Sitter) द्वारा प्रस्तावित की गई[३]:
- <math>c'=c\pm kv\,</math>
यहाँ c प्रकाश का वेग, v स्रोत का वेग, c′ प्रकाश का परिणामी वेग है और k एक नियतांक है जिसका मान ० से १ के मध्य हो सकता है और यह स्रोत के क्षत्र पर निर्भर करता है। विशिष्ठ आपेक्षिकता सिद्धांत व स्थिर ईथर के अनुसार k=0 होता है जबकि उत्सर्जन सिद्धांत के अनुसार यह मान 1 तक हो सकता है। अनेक भौमिक प्रयोग बहुत लघु दूरियों पर किये गये, जहाँ कोई ईथर घसीटने अथवा कोई अन्य प्रभाव प्रभावी ना हो और पुनः परिणामों में यही प्रदर्शित हुआ कि प्रकाश का वेग स्रोत पर निर्भर नहीं करता, परिणामस्वरूप उत्सर्जन सिद्धान्तों का खण्डन हो गया।
खगोलीय स्रोत
डेनियल फ्रॉस्ट कॉम्सटोक व विलियम डी सिटर ने १९१० में लिखा कि द्वि-तारा सम्बन्धी सिद्धन्त कुछ सही प्रतीत हो रहा है, निकट आ रहे तारे से उत्सर्जित प्रकाश अपने सहचर से उत्सर्जित प्रकाश से तेज गति से आगे बढना चाहिए और इससे आगे निकल जाना चाहिए। इन परिस्थितियों में तारक तन्त्र का चित्र एकदम एक दूसरे को पार करते हुये होनी चाहिए। डी सिटेर के अपने अध्ययन में पाया कि कोई भी तारा तन्त्र इस चरम प्रभाव जैसा व्यवहार नहीं करता, व्यापक रूप से यह ॠत्जियन सिद्धान्त का अन्त माना गया जहाँ <math>k < 2\times10^{-3}</math>.[३][४][५]
भौमिक स्रोत
व्यतिकरणमापी
अन्य खण्डन
सन्दर्भ
- आइज़क न्यूटन, फिलासफी नेचुरालिस् प्रिंसिपिया मैथेमैटिका।
- आइज़क न्यूटन, ऑप्टिक्स (Opticks)
- ↑ स्क्रिप्ट त्रुटि: "citation/CS1" ऐसा कोई मॉड्यूल नहीं है।
- ↑ स्क्रिप्ट त्रुटि: "citation/CS1" ऐसा कोई मॉड्यूल नहीं है।
- ↑ अ आ स्क्रिप्ट त्रुटि: "citation/CS1" ऐसा कोई मॉड्यूल नहीं है।
- ↑ स्क्रिप्ट त्रुटि: "citation/CS1" ऐसा कोई मॉड्यूल नहीं है।
- ↑ स्क्रिप्ट त्रुटि: "citation/CS1" ऐसा कोई मॉड्यूल नहीं है।