आवृत्ति मॉड्यूलेशन

संकेतों को आयाम-मॉडुलन (AM) करके प्रसारित किया जा सकता है और आवृत्ति मॉड्यूलेशन (FM) करके भी।

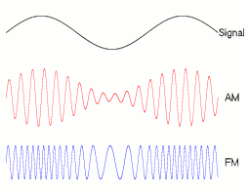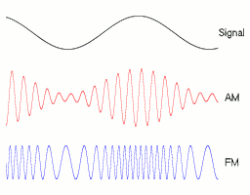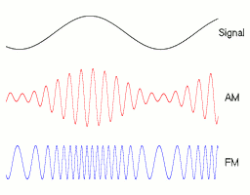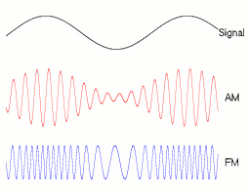
आवृत्ति मॉडुलन (फ़्रिक्वेंसी मॉड्यूलेशन), मॉडुलन का एक प्रकार है जहाँ मॉड्यूलेटिंग संकेत के आयाम अनुसार के वाहक की तात्क्षणिक आवृत्ति बदली जाती है और इस वाहक का आयाम अपरिवर्ती बना रहता है। इसका उपयोग अनेक स्थानों पर होता है जैसे- दूरसंचार, रेडियो प्रसारण, संकेत प्रसंस्करण, तथा संगणन (कम्युटिंग) में। आवृत्ति मॉडुलित संकेतों प्र रव (noise) का प्रभाव कम पड़ता है। दूसरे शब्दों में कहें तो डिमॉडुलन के पश्चात जो मूल संकेत प्राप्त किया जाता है उसमें रवों का प्रभाव नगण्य रह जाता है।

सिद्धान्त

माना जिस संकेत को प्रसारित करना है (अर्थात, बेसबैण्ड संकेत) वह <math>x_m(t)</math> है तथा साइन-आकारी वाहक संकेत <math>x_c(t) = A_c \cos (2 \pi f_c t)\,</math> है, जहाँ f_c वाहक की आधार (बेस) आवृत्ति है तथा A_c वाहक का आयाम है। मॉडुलक (modulator) इन दोनों संकेतों को मिलाकर एक नया संकेत बनाता है जिसे 'आवृत्ति मॉडुलित' संकेत कहते हैं।

<math>\begin{align}

 y(t) &= A_c \cos\left(2\pi \int_0^t f(\tau) d\tau\right) \\
      &= A_c \cos\left(2\pi \int_0^t \left[f_c + f_\Delta x_m(\tau)\right] d\tau\right) \\ 
      &= A_c \cos\left(2\pi f_c t + 2\pi f_\Delta \int_0^t x_m(\tau) d\tau\right) \\ 

\end{align}</math>

जहाँ <math>f_\Delta = K_f A_m</math>, <math>K_f</math> आवृत्ति मॉडुलक की सुग्राहिता (sensitivity) है तथा <math>A_m</math> मॉडुलक संकेत (या, बेसबैण्ड संकेत) का आयाम है।

इस समीकरण में, <math>f(\tau)\,</math> ऑसिलेटर की तात्क्षणिक आवृत्ति है तथा <math>f_\Delta\,</math> आवृत्ति विचलन है, जो बताता है कि f_c से एक दिशा में अधिक से अधिक कितना परिवर्तन हो सकता है, यह मानते हुए कि x_m(t) का मान ±1 की सीमा में रहता है।

आवृत्ति मॉडुलित संकेत की अधिकांश ऊर्जा f_c ± f_Δ में निहित होती है। फुर्रे विश्लेषण (Fourier analysis) द्वार यह दर्शाया जा सकता है कि किसी FM संकेत को निरूपित करने के लिये अपेक्षाकृत इससे अधिक आवृत्ति आवश्यक होती है।

इन्हें भी देखें

• मॉडुलन