अनुप्रस्थ तरंग

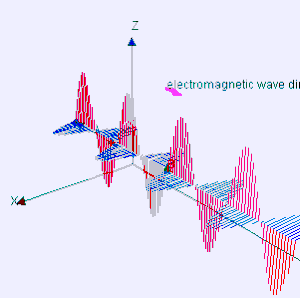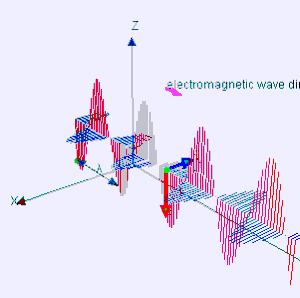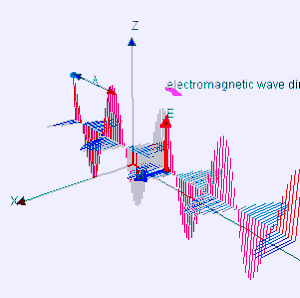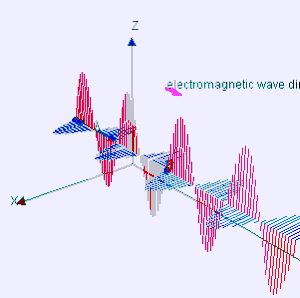
अनुप्रस्थ तरंग उस तरंग को कहते हैं जिसके दोलन तरंग संचरण की दिशा के लम्बवत होते हैं। इस दृष्टि से अनुप्रस्थ तरंगें, अनुदैर्घ्य तरंगों से अलग हैं जिनमें तरंग की गति दोलन के दिशा में ही होती है। विद्युतचुम्बकीय तरंगें (जैसे प्रकाश, ऊष्मा आदि) अनुप्रस्थ तरंगे होतीं हैं।

अनुप्रस्थ तरंग

यदि एक डोरी लेकर उसके एक सिरे को एक बिन्दु पर बांध दिया जाय, तथा दूसरे सिरे को खींचकर रखते हुए ऊपर-नीचे किया जाय तो इस डोरी में एक अनुप्रस्थ यांत्रिक तरंग स्थापित हो जाती है। इसी प्रकार, ढोलक की तनी हुई झिल्ली पर थाप लगाने से जो तरंग पैदा होती है वह भी अनुप्रस्थ तरंग ही होती है क्योंकि झिल्ली के विभिन्न विन्दुओं का दोलन झिल्ली के तल के लम्बवत होता है जबकि झिल्ली पर स्थापित तरंग झिल्ली के तल की दिशा में गति करती है।

एक सामान्य प्रकाश तरंग में विद्युत क्षेत्र तथा चुम्बकीय क्षेत्र दोनों ही प्रकाश की गति के लम्बवत होते हैं।

गणितीय निरूपण

समतल रैखिक ध्रुवित साइन तरंग

गणितीय निरूपण की दृष्टि से अनुप्रस्थ तरंग का सबसे सरल उदाहरण समतल "रैखिक ध्रुवित साइन तरंग" (plane linearly polarized sinusoidal) है। इसमें 'समतल' का अर्थ है कि तरंग की गति अपरिवर्तित है तथा पूरे माध्यम में (सर्वत्र) एक ही है ; रैखिक ध्रुवित (linearly polarized) का अर्थ है कि पूरे माध्यम में विस्थापन की दिशा भी अपरिवर्तित रहती है; तथा विस्थापन का परिमाण केवल समय और तरंग की गति की दिशा में स्थिति का साइन (sinusoidal function ) फलन है।

ऐसे तरंग की गति को निम्नलिखित प्रकार से अभिव्यक्त किया जा सकता है-

<math>S(p,t)=Au\sin{\left(\frac{t-(p-o)\cdot\frac{d}{v}}{T}+\phi\right)}</math>

जहाँ p किसी समय t (seconds) पर कण का विस्थापन है। d तरंग-गति की दिशा में इकाई सदिश है, तथा o माध्यम में स्थित कोई सन्दर्भ बिन्दु है। माना u दोलन की दिशा में एक ईकाई-सदिश है (d के लम्बवत)। A तरंग का आयाम है, T इसका आवर्तकाल है, v तरंग की चाल है, φ इस तरंग की o बिन्दु पर कला (फेज) है। ये सभी पैरामीटर वास्तविक हैं और संकेत "•" दो सदिशों के आन्तरिक गुणनफल को अभिव्यक्त करता है।

कोई प्रेक्षक यदि किसी नियत बिन्दु p पर देखता है तो उसको उस बिन्दु पर स्थित कण सरल आवर्त गति करते हुए मालूम चलेंगे जिसका आवर्तकाल T सेकेण्ड, और अधिकतम विस्थापन A है।

बाहरी कड़ियाँ

• [१]