अनुपात परीक्षा
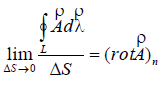 अनुपात
गणित में अनुपात परीक्षा (ratio test) किसी श्रेणी के अभिसरण की जाँच के लिये प्रयुक्त होता है। यह परीक्षण सर्वप्रथम डी अलम्बर्ट (Jean le Rond d'Alembert) ने प्रकाशित किया था।
अनुपात
गणित में अनुपात परीक्षा (ratio test) किसी श्रेणी के अभिसरण की जाँच के लिये प्रयुक्त होता है। यह परीक्षण सर्वप्रथम डी अलम्बर्ट (Jean le Rond d'Alembert) ने प्रकाशित किया था।
परिचय
माना श्रेणी <math>\sum_{n=0}^\infty a_n</math> है, जहाँ प्रत्येक पद वास्तविक संख्या या समिश्र संख्या है तथा जब n अनन्त की ओर अग्रसर होता है तब <math>a_n</math> अशून्य संख्या है। इस श्रेणी के अभिसरण के बारे में जानकारी यह परीक्षण निम्नांकित सीमा के मान (value) के आधार पर देता है-
<math>L=\lim_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|</math>,
अनुपात परीक्षा कहती है कि:
- यदि L < 1 तो श्रेणी पूर्णतः अभिसारी है।
- यदि L > 1 तो श्रेणी अभिसारी नहीं है।
- यदि L = 1 हो या सीमा का अस्तित्व नहीं है तो यह परीक्षण अभिसरण के बारे में ठीक-ठीक कुछ भी नहीं कह सकता, अर्थात् कोई निश्चित निष्कर्ष नहीं निकालता।
उदाहरण
अभिसारी श्रेणी (L<1)
निम्नलिखित श्रेणी लीजिये-
- <math>\sum_{n=1}^\infty\frac{n}{e^n}</math>
इस पर अनुपात परीक्षा करने पर,
- <math>L = \lim_{n\to\infty} \left| \frac{a_{n+1}}{a_n} \right|
= \lim_{n\to\infty} \left| \frac{\frac{n+1}{e^{n+1}}}{\frac{n}{e^n}}\right| = \frac{1}{e} < 1.</math>
अतः श्रेणी अभिसारी है।
अपसारी श्रेणी (L>1)
निम्नलिखित श्रेणी लीजिये-
- <math>\sum_{n=1}^\infty\frac{e^n}{n}.</math>
इस पर अनुपात परीक्षा करने पर,
- <math>L
= \lim_{n\to\infty} \left| \frac{a_{n+1}}{a_n} \right| = \lim_{n\to\infty} \left| \frac{\frac{e^{n+1}}{n+1}}{\frac{e^n}{n}} \right| = e > 1.</math>
अतः श्रेणी अपसारी है।
अनिर्णीत स्थिति (L=1)
निम्नलिखित तीन श्रेणियों को देखिये-
- <math>\sum_{n=1}^\infty 1,</math> <math>\sum_{n=1}^\infty \frac{1}{n^2}</math> तथा <math>\sum_{n=1}^\infty (-1)^n\frac{1}{n}</math>.
यद्यपि <math>\left|\frac{a_{n+1}}{a_n}\right|</math> का मान क्रमशः 1, <math>\frac{n^2}{(n+1)^2}</math> तथा <math>\frac{n}{n+1}</math> हैं और तीनो स्थितियों में <math>\lim_{n\rightarrow\infty}\left|\frac{a_{n+1}}{a_n}\right|=1</math> किन्तु पहली श्रेणी अपसारी है, दूसरी श्रेणी पूर्णतः अभिसारी है तथा तीसरी श्रेणी शर्त के साथ अभिसारी है।
. इससे स्पष्ट है कि जब L=1, तो श्रेणी अभिसारी या अपसारी कुछ भी हो सकती है।
