अनंतस्पर्शी
वैश्लेषिक ज्यामिति में किसी वक्र की अनन्तस्पर्शी (asymptote) उस रेखा को कहते हैं जो उस वक्र को अनन्त पर स्पर्श करती हुई प्रतीत होती है। अर्थात् ज्यों-ज्यों वक्र तथा वह रेखा अनन्त की ओर अग्रसर होते हैं, त्यों-त्यों उनके बीच की दूरी शून्य की ओर अग्रसर होती है। कुछ संदर्भों में मोटे तौर पर कह दिया जाता है कि, 'किसी वक्र की अनन्त पर स्पर्शरेखा उस वक्र की अनंतस्पर्शी कहलाती है।'
अनन्तस्पर्शी के ज्ञान से वक्रों के आरेखण में बहुत सहायता मिलती है क्योंकि अनन्तस्पर्शी वक्रों का बहुत दूरी पर स्थिति का संकेत करती है।
उदाहरण
अतिपरवलय (Hyperbola)
- <math>
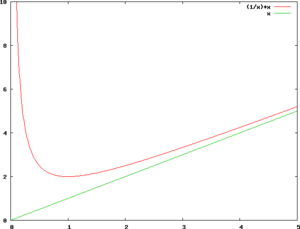
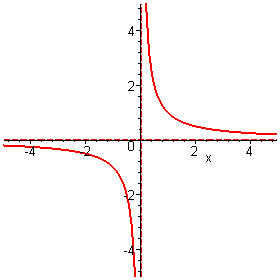
f_1(x) = \frac{1}{x}
</math> की दो अनन्तस्पर्शी हैं; x = 0 तथा y = 0.
फलन
- <math>
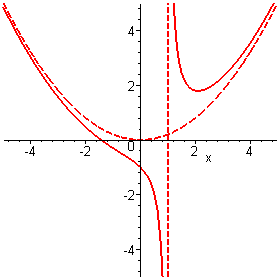
f_2(x) = \frac{x^3-x^2+5}{5x-5} = \frac{x^3-x^2}{5x-5}+ \frac{1}{x-1}
= \frac{1}{5}x^2 + \frac{1}{x-1} </math> की भी दो अनन्तस्पर्शियाँ हैं - सरल रेखा x = 1 तथा परवलय <math>p(x) = \frac{1}{5}x^2</math> (यदि हम मानें कि सरलरेखा के अलावा अन्य वक्र भी अनन्तस्पर्शी के रूप में स्वीकार्य हैं।)
वक्र का अनुरेखण
साँचा:main वक्र का समीकरण दिए रहने पर वक्र का अनुरेखन संभव होता है। चरों के ऐसे संगत मान ज्ञात करके, जिसे समीकरण संतुष्ट हो जाए, उन अनेक बिंदुओं का पता लग सकता है जिनसे वक्र गुजरता है। इन बिंदुओं को जोड़ने पर वक्र की एक मोटी रूपरेखा का पता लग जाता है। फिर भी कुछ ऐसी बातें होती हैं जिनसे उसके आकार प्रकार, लक्षण, स्वरूप आदि जानने में आसानी हो जाती हैं, जैसे :
- (क) सममिति (Symmetry) - यदि वक्र के समीकरण में y का कोई विषमघात नहीं है, तो वक्र x-अक्ष के प्रति सममित होगा। यदि x का कोई विषमघात नहीं है, तो वक्र Y-अक्ष के प्रति सममित होगा, तथा x और y दोनों का कोई विषमघात नहीं है, तो वक्र दोनों अक्षों के प्रति सममित होगा। यदि x और y को क्रमश: -x और -y रखने से समीकरण में कोई अंतर नहीं पड़ता है, तो वक्र सम्मुख चतुर्थांशों में सममित होगा। x और y के विनिमय (interchange) से समीकरण यदि अपरिवर्तित रहता है, तो वक्र y = x रेखा के प्रति सममित होगा। ध्रुवी समीकरण में q को -q रखने से यदि कोई अंतर नहीं पड़ता है, तो वक्र आदि रेखा के प्रति सममित होगा। यदि r का कोई विषमघात नहीं है, तो वक्र मूल के प्रति सममित होगा और ध्रुव एक केंद्र होगा।
- (ख) अनंतस्पर्शी - इनकी संख्या और वक्र के सापेक्ष इनकी स्थिति।
- (ग) वक्र के नतिपरिवर्तन बिंदु, बहुल बिंदु, कस्प, नोड आदि तथा इनकी संख्या और स्वरूप।
- (घ) वक्र और अक्ष जहाँ कटते हैं, उन बिंदुओं पर वक्र की स्थिति और स्पर्श रेखाओं की दिशा आदि।
- (च) मूल परस्पर्शी, वक्र के सापेक्ष उसकी स्थिति, विचित्रता आदि, यदि वक्र मूल से गुजरता हो।
- (छ) वक्र की सीमाएँ।