अधिकतम शक्ति अन्तरण प्रमेय
विद्युत प्रौद्योगिकी में विद्युत परिपथ सम्बन्धी यह महत्त्वपूर्ण प्रमेय है। इसके अनुसार यदि स्रोत का इम्पीडेन्स (प्रतिबाधा) नियत हो और लोड की प्रतिबाधा बदलने की स्वतन्त्रता हो तो स्रोत से लोड को अधिकतम शक्ति उस दशा में हस्तानान्तरित होगी जब लोड का इम्पीडेन्स स्रोत के इम्पीडेन्स का समिश्र युगल (complex conjugate) के बराबर हो। इसे ही अधिकतम शक्ति (हस्तानान्तरण) प्रमेय (maximum power (transfer) theorem) कहते हैं।
ऐसा दावा किया जाता है कि जैकोबी (Moritz von Jacobi) ने सबसे पहले इसका आविष्कार किया।
- विशेष
- यह ध्यातब्य है कि यह प्रमेय अधिकतम शक्ति के बारे में है, अधिकतम दक्षता के बारे में नहीं। महत्तम शक्ति ट्रान्सफर की दशा में स्रोत से उत्पन्न कुल शक्ति का केवल ५०% ही लोड को स्थानातरित होता है। (अर्थात दक्षता=५०%)
- इसमें स्रोत का इम्पीडेन्स दिया हुआ है (या, नियत है); लोड का इम्पीडेन्स बदलने की स्वतन्त्रता है। किन्तुइसके विपरीत लोड की इम्पीडेन्स नियत हो और स्रोत का इम्पीडेन्स बदलने की स्वतन्त्रता हो तो स्रोत से लोड को अधिकतम शक्त उस दश्आ में ट्रान्सफर होगी जब स्रोट का इम्पीडेन्स शून्य हो जाय।
- शक्तिशाली परिपथों (पॉवर सर्किट्स) में कभी भी महत्तम शक्ति हस्तानातरण की बात नहीं की जाती है न ही इसकी कामना की जाती है। क्योंकि शक्ति-परिपथों में दक्षता बहुत महत्व की है; अधिकतम शक्ति का हस्तानान्तरण कोई मुद्दा ही नहीं होता।
- इसी प्रकार अधिकतर संचार परिपथों में भीइसका उपयोग नहीं किया जाता - अधिकांश परिपथों के ऑउटपुट इम्पीडेन्स बहुत कम होते हैं और उनके इनपुट इम्पीडेन्स बहुत अधिक।
- अधिकतम शक्ति ट्रान्सफर के लिये इम्पीडेन्स-मैचिंग कुछ ही स्थानों व्यावहारिक रूप से उपयोगी होता है। उदाहरण के लिये आर-एफ् पॉवर एम्प्लिफायर के ऑउटपुत को एन्टेना के इम्पीडेन्स से मैच कराया जाता है।
महत्तम शक्ति एवं महत्तम दक्षता (Maximizing power transfer versus power efficiency)
अधिकतम शक्ति ट्रान्सफर की दशा में अधिकतम दक्षता की प्राप्ति नहीं होती। यदि हम दक्षता (efficiency) <math>\eta</math> को लोड को प्राप्त शक्ति एवं स्रोत से उत्पन्न शक्ति के अनुपात (रेशियो) के रूप में परिभाषित करें तो,
- <math>
\eta = {R_\mathrm{load} \over {R_\mathrm{load} + R_\mathrm{source} } } = { 1 \over { 1 + { R_\mathrm{source} \over R_\mathrm{load} } } } </math>
इन तीन दशाओं पर विचार कीजिये:
- यदि <math>R_\mathrm{load}=R_\mathrm{source}</math>, तो <math>\eta=0.5</math>.
- यदि <math>R_\mathrm{load}=\infty</math> or <math>R_\mathrm{source} = 0</math>, तो <math>\eta=1</math>.
- यदि <math>R_\mathrm{load}=0</math>, तो <math>\eta=0</math>.
इस प्रकार स्पष्ट है कि जब अधिकतम शक्ति लोड को हस्तानान्तरित होती है तब दक्षता केवल ५०% ही है।
पूर्णतः प्रतिरोधात्मक परिपथ के लिये कैलकुलस पर आधारित उपपत्ति
(See Cartwright[१] for a non-calculus-based proof)
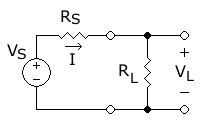
सामने के चित्र में, <math>V</math> वोल्टता एवं नियत स्रोत प्रतिरोध (source resistance]) <math>R_\mathrm{S}</math> वाले स्रोत से एक <math>R_\mathrm{L}</math> प्रतिरोध वाले लोड में विद्युत शक्ति दी जा रही है। इससे लोड में <math>I</math> धारा प्रवाहित हो रही है। ओम के नियम के अनुसार <math>I</math> का मान स्रोत वोल्टता को कुल प्रतिरोध से भाग करने पर प्राप्त संख्या के बराबर होगा।
- <math>
I = {V \over R_\mathrm{S} + R_\mathrm{L}}. </math>
लोड में व्यय हुई शक्ति <math>P_\mathrm{L}</math> धारा के वर्ग एवं लोड के प्रतिरोध के गुणनफल के बराबर होगी।
- <math>
P_\mathrm{L} = I^2 R_\mathrm{L} = {{ \left({V \over {R_\mathrm{S} + R_\mathrm{L}}} \right) }^2} R_\mathrm{L} = {{V^2} \over {R_\mathrm{S}^2 / R_\mathrm{L} + 2R_\mathrm{S} + R_\mathrm{L}}}. </math>
अब हम <math>R_\mathrm{L}</math> का वह मान निकाल सकते हैं जिसके लिये शक्ति का यह व्यंजक महत्तम मान ग्रहण करतअ है। इसके बजाय <math>R_\mathrm{L}</math> का वह मान ज्ञात करना अधिक आसान है जिसके लिये इस व्यंजक का हर (denominator) न्यूनतम हो। दोनो ही दशाओं में एक ही परिणाम मिलेगा।
- <math>
R_\mathrm{S}^2 / R_\mathrm{L} + 2R_\mathrm{S} + R_\mathrm{L} </math>
<math>R_\mathrm{L}</math> के सापेक्ष अवकलन करने पर,
- <math>
{d\over{dR_\mathrm{L}}} \left({R_\mathrm{S}^2 / R_\mathrm{L} + 2R_\mathrm{S} + R_\mathrm{L}} \right) = -R_\mathrm{S}^2 / R_\mathrm{L}^2+1. </math>
अधिअकतम या न्यूनतम (maximum or minimum) के लिये पहला अवकलज शून्य होना चाहिये।
- <math>
{R_\mathrm{S}^2 / R_\mathrm{L}^2} = 1 </math>
or
- <math>R_\mathrm{L} = \pm R_\mathrm{S}.</math>
व्यावहारिक परिपथों में <math>R_\mathrm{S}</math> एवं <math>R_\mathrm{L}</math> दोनो ही धनात्मक (positive.) मान वाले होते हैं। यह जानने के लिये कि प्राप्त परिणाम अधिकतम देता है या न्यूनतम, एक बार और अवकलन करने पर-
- <math>{{d^2} \over {dR_\mathrm{L}^2}} \left({R_\mathrm{S}^2 / R_\mathrm{L} + 2 R_\mathrm{S} + R_\mathrm{L}} \right) = {2 R_\mathrm{S}^2} / {R_\mathrm{L}^3}</math>
<math>R_\mathrm{S}</math> एवं <math>R_\mathrm{L}</math> के धनात्मक मानों के लिये यह धनात्मक है। इसका अर्थ है कि उक्त हर उपर्युक्त दशा में न्यूनतम होगा; अर्थात शक्ति का मान महत्तम होगा।
- <math>R_\mathrm{S} = R_\mathrm{L}.</math>
रिएक्टिव परिपथों के लिये (In reactive circuits)
यह प्रमेय उस दशा में भी सत्य है जब स्रोत एवं लोड के इम्पीडेन्स पूर्ण्तः प्रतिरोधात्मक नहीं हैं बल्कि रिएक्टिव प्रकृति के हैं।
प्रतिबाधा सुमेलन (Impedance matching)
स्क्रिप्ट त्रुटि: "main" ऐसा कोई मॉड्यूल नहीं है। रेडियो, ट्रान्समिशन लाइनों एवं कुछ एलेक्ट्रॉनिक परिपथों में प्रायः ऐसी जरूरत होती है कि लोड (जैसे एन्टेना) का इम्पीडेन्स स्रोत (जैसे ट्रान्समिटर) के इम्पीडेन्स के बराबर रखा जाय। इससे ट्रान्समिसन लाइन में रिफ्लेक्शन (परावर्तन) की समस्या नहीं होता।
इन्हें भी देखें
- प्रतिबाधा सुमेलन (इम्पीडेन्स मैचिंग)
टिप्पणियाँ
सन्दर्भ
- H.W. Jackson (1959) Introduction to Electronic Circuits, Prentice-Hall.
बाहरी कड़ियाँ
- The complex conjugate matching false idol
- Conjugate matching versus reflectionless matching (PDF) taken from Electromagnetic Waves and Antennas
- The Spark Transmitter. 2. Maximising Power, part 1.
- Jacobi's theorem - unconfirmed claim that theorem was discovered by Moritz Jacobi
- [१] MH Jacobi Biographical notes
- Google Docs Spreadsheetसाँचा:category handlerसाँचा:main otherसाँचा:main other[dead link] calculating max power transfer efficiencies by Sholto Maud and Dino Cevolatti.