पूँजीगत परिसम्पत्ति कीमत निर्धारण मॉडल

वित्त में, पूँजीगत परिसम्पत्ति कीमत निर्धारण मॉडल (capital asset pricing model सी॰ए॰पी॰एम॰) का उपयोग किसी पूँजीगत परिसम्पत्ति के लिए सैद्धांतिक रूप से उपयुक्त वांछित प्रतिलाभ दर ज्ञात करने के लिए किया जाता है, जब इस परिसम्पत्ति को एक पहले से ही सुविशाखीकृत संविभाग (अच्छी तरह से डाईवर्सिफाईड पोर्टफोलियो) में जोड़ा जाना हो, तथा जबकि उस परिसम्पत्ति का अशाखनीय जोखिम (non-diversifiable risk) ज्ञात हो। इस मॉडल में परिसंपत्ति के अशाखनीय जोखिम (व्यवस्थात्मक जोखिम या बाज़ार जोखिम) जिसे वित्त क्षेत्र में प्रायः 'बीटा' (β) के द्वारा प्रदर्शित किया जाता है, को गणना में लिया जाता है तथा बाजार के प्रत्याशित प्रतिलाभ व सैद्धांतिक जोखिम-मुक्त परिसंपत्ति के प्रत्याशित प्रतिलाभ को भी। सी॰ए॰पी॰एम॰ का सुझाव है कि किसी निवेशक की शेयर पूँजी की लागत का निर्धारण 'बीटा' (β) से होता है। ”[१]साँचा:rp इस मॉडल का विस्तृत रूप द्वि-बीटा मॉडल है, जो कि उर्ध्वगामी बीटा को अधिगामी बीटा से भिन्न करता है।[२]
सी॰ए॰पी॰एम॰ की अवधारणा, हैरी मार्कोविट्ज़ द्वारा विशाखीकरण/विविधीकरण तथा आधुनिक संविभाग थियोरी पर पहले किए गए कार्य का विस्तार करते हुए, जैक ट्रेयनॉर (1961, 1962),[३] विलियम शार्पे (1964), जॉन लिन्टनर (1965a,b) and जान मोसिन (1966) द्वारा स्वतंत्र रूप से प्रस्तुत की गई। 1990 में शार्पे, मार्कोविट्ज़ व मर्टन मिलर को संयुक्त रूप से वित्तीय अर्थशास्त्र में योगदान के लिए नोबेल पुरस्कार से सम्मानित किया गया। फिशर ब्लैक (1972) ने सी॰ए॰पी॰एम॰ का एक और संस्करण, ब्लैक सी॰ए॰पी॰एम॰ या शून्य-बीटा सी॰ए॰पी॰एम॰, विकसित किया जिसमें जोखिम-मुक्त परिसंपत्ति की मान्यता को खारिज किया गया था। empirical testing में यह संस्करण अधिक दृढ़ था तथा सी॰ए॰पी॰एम॰ की वैश्विक स्वीकृति में इसका प्रभावी योगदान रहा।
मूल्य निर्धारण व पोर्टफोलियो चयन के कई आधुनिक तरीकों (जैसे अंतरपणन कीमत सिद्धांत व मर्टन पोर्टफोलियो समस्या, क्रमशः) के आगमन तथा अंतरपणन आनुभविक खामियों, के बावजूद अपनी साधारणता व विभिन्न प्रकार परिस्थितियों में उपयोगिता के कारण सी॰ए॰पी॰एम॰ अभी भी अधिक प्रचलित है।
सूत्र
यह सम्पूर्ण पृष्ठ या इसके कुछ अनुभाग हिन्दी के अतिरिक्त अन्य भाषा(ओं) में भी लिखे गए हैं। आप इनका साँचा:edit करके विकिपीडिया की सहायता कर सकते हैं। |
सी॰ए॰पी॰एम॰ किसी अकेली परिसंपत्ति अथवा परिसंपत्तियों के समूह (पोर्टफोलियो) की कीमत निर्धारण करने के लिए एक मॉडल है। अकेली प्रतिभूति के लिए, हम प्रतिभूति बाजार रेखा (security market line, SML) तथा प्रत्याशित प्रतिलाभ व सिस्टेमैटिक जोखिम के साथ उसके संबंध (बीटा) का प्रयोग यह जानने के लिए करते हैं कि बाजार के द्वारा किसी एक प्रतिभूति की कीमत उसकी जोखिमश्रेणी की तुलना में कितनी निर्धारित होगी। प्रतिभूति बाजार रेखा से किसी एक संपत्ति की पूरे बाजार की तुलना में प्रतिफल-जोखिम अनुपात की गणना भी की जा सकती है। अतः जैसे जैसे किसी संपत्ति का प्रत्याशित प्रतिलाभ उसके बीटा कोफिशेन्ट द्वारा घटता चला जाएगा, इस अकेली संपत्ति का प्रतिफल-जोखिम अनुपात, संपूर्ण बाजार के प्रतिफल-जोखिम अनुपात के बराबर होता चला जाएगा। इस प्रकार:
- <math>\frac {E(R_i)- R_f}{\beta_{i}} = E(R_m) - R_f </math>
बाजार का प्रतिफल-जोखिम अनुपात ही प्रभावी तौर पर बाजार जोखिम अधिमूल्य/प्रीमियम है और उपरोक्त समीकरण को पुनः नियोजन करने पर तथा E(Ri) का मान निकालने पर, हमें पूँजीगत परिसम्पत्ति कीमत निर्धारण मॉडल (सी॰ए॰पी॰एम॰) प्राप्त हो जाता है।
- <math>E(R_i) = R_f + \beta_{i}(E(R_m) - R_f)\,</math>
जहाँ:
- <math>E(R_i)~~</math> है - पूँजी परिसंपत्ति पर प्रत्याशित प्रतिफल
- <math>R_f~</math> है - जोखिम-मुक्त ब्याज दर (जैसे कि सरकारी प्रतिभूतियों पर मिलने वाला ब्याज)
- <math>\beta_{i}~~</math> (बीटा) है - 'परिसंपत्ति के प्रत्याशित अतिरिक्त प्रतिफल' की 'बाजार के प्रत्याशित अतिरिक्त प्रतिफल' के प्रति संवेदनशीलता, या <math>\beta_{i} = \frac {\mathrm{Cov}(R_i,R_m)}{\mathrm{Var}(R_m)}</math> भी लिख सकते हैं।
- <math>E(R_m)~</math> है - बाजार का प्रत्याशित प्रतिफल
- <math>E(R_m)-R_f~</math> है - बाजार अधिमूल्य/प्रीमियम (बाजार की प्रत्याशित प्रतिफल दर तथा जोखिम मुक्त प्रतिफल दर का अन्तर)
- <math>E(R_i)-R_f~</math> है - जोखिम अधिमूल्य/प्रीमियम
यदि इसी को जोखिम प्रीमियम के दृष्टिकोण से पुनर्लेखित किया जाए, तो हम पाते हैं कि:
- <math>E(R_i) - R_f = \beta_{i}(E(R_m) - R_f)\,</math>
अर्थात् किसी परिसंपत्ति का "अपना जोखिम प्रीमियम"- "बाजार जोखिम प्रीमियम" व "बीटा" (β) का गुणनफल है।
नोट 1: बाजार के प्रत्याशित प्रतिफल का अनुमान प्रायः किसी बाजार-पोर्टफोलियो (जैसे कि कोई शेयर सूचकाँक) के एतिहासिक प्रतिफलों के मान का ज्योमैट्रिक औसत निकालकर लगाया जाता है।
नोट 2: जोखिम की गणना हेतु प्रयुक्त 'जोखिम मुक्त प्रतिफल दर' प्रायः एतिहसिक दरों का arithmetic औसत होता है ना कि वर्तमान दर।
For the full derivation see Modern portfolio theory.
अंशातरित सूत्र
सी॰ए॰पी॰एम॰ को आमाप अधिवेतन और विशिष्ट जोखिम शामिल करने के लिए संशोधित किया जा सकता है। यह उन निवेशकों के लिए महत्वपूर्ण है जिनके पास एक उन्नत-विशाखित पोर्टफोलियो नहीं है। समीकरण पारम्परिक सी॰ए॰पी॰एम॰ समीकरण के समान ही है “जिसमें बाजार जोखिम अधिवेतन को बीटा उत्पा और बाजार जोखिम अधिवेतन के गुणा से प्रतिस्थापित कर दिया गया है:”[१]साँचा:rp
- <math>E(R_i) = R_f + \beta(RP_m) + RP_s + RP_u</math>
"जहाँ:
- <math>E(R_i)</math> सुरक्षा i पर अपेक्षित प्रतिदान (वापसी) है।
- <math>R_f</math> जोखिम-रहित दर है
- <math>RP_m</math> सामान्य बाजार जोखिम अधिवेतन है
- <math>RP_s</math> लघु उधमों के लिए जोखिम अधिवेतन है
- <math>RP_u</math> कम्पनी अथवा संगठन के जोखिम गुणांक के कारण जोखिम अधिवेतन है।"[१]साँचा:rp
प्रतिभूति बाज़ार रेखा
प्रतिभूति बाज़ार रेखा (Security market line,SML) सी॰ए॰पी॰एम॰ के फार्मूला का ग्राफ के रूप में चित्रण करती है। x अक्ष पर जोखिम (बीटा) को दिखाते हैं और y अक्ष पर प्रत्याशित प्रतिलाभ। बाजार जोखिम का अनुमान प्रतिभूति बाज़ार रेखा की ढलान (स्लोप) से लगाया जाता है।
β तथा प्रत्याशित प्रतिलाभ के मध्य संबंध का चित्रण प्रतिभूति बाज़ार रेखा (SML) पर किया जाता है, जो कि प्रत्याशित प्रतिलाभ को β के फलन के रूप में प्रदर्शित करता है। The intercept is the बाजार में उपलब्ध nominal जोखिम मुक्त दर है, जबकि ढलान market premium है, E(Rm)− Rf। एसा कहा जा सकता है कि प्रतिभूति बाज़ार रेखा as representing a single-factor model of the asset price को दिखाती है, जबकि β से पता चलता है कि उसकी बाजार में परिवर्तनों से प्रभावित होने की संभावना कितनी है (where Beta is exposure to changes in value of the Market.) इस प्रकार SML का समीकरण इस प्रकार है:
- <math> \mathrm{SML}: E(R_i)= R_f+\beta_i (E(R_M) - R_f).~ </math>
ऐसी परिस्थितियों के लिए यह एक अति महत्वपूर्ण टूल है जब पता करना हो कि क्या (पोर्टफोलियों में सम्मिलित करने हेतु विचाराधीन) कोई परिसमपत्ति/प्रतिभूति जोखिम की तुलना में एक स्वीकार्य प्रतिफल देगी कि नहीं। अकेली परिसंपत्तियों का चित्रण प्रतिभूति बाज़ार रेखा ग्राफ पर किया जाता है। यदि जोखिम व प्रतिफल का परस्पर चित्रण रेखा से ऊपर होता है तो इसका अर्थ है कि यह प्रतिभूति सस्ती मिल रही है और इस पर अधिक लाभ की उम्मीद की जा सकती है। यदि चित्रण रेखा से नीचे आ पड़े तो मूल्य को मंहगा समझा जाना चाहिए तथा इसमें उतना लाभ नहीं मिलेगा जितना कि जोखिम उठाया जा रहा है।
परिसम्पत्ति कीमत निर्धारण
सीएपीम का उपयोग करते हुए प्रत्याशित/वाँछित लाभदर <math>E(R_i)</math> ज्ञात होने के पश्चात् इसकी तुलना संपत्ति के अनुमानित प्रतिलाभ दर (किसी निश्चित अंतराल में) से करके यह पता लगा सकते हैं कि यह निवेश अच्छा रहेगा कि नहीं। इसके लिए हमें संपत्ति के प्रतिलाभ के स्वतंत्र अनुमान की गणना की आवश्यकता होगी जो कि प्रायः फंडामेंटल अथवा टेक्निकल विश्लेषण, आनुपातिक विश्लेषण (मूल्य/आय- Price/Earning, बाजार मूल्य/आंतरिक मूल्य - Market Price/Book Value ) आदि के द्वारा की जाती है।
सी॰ए॰पी॰एम॰ के अनुसार, यदि अनुमानित मूल्य, संपत्ति के सी॰ए॰पी॰एम॰ द्वारा सुझाई दर के साथ समायोजित किए गए भविष्य नकदप्रवाह के बराबर है - तो संपत्ति सही मूल्य पर मिल रही है। यदि अनुमानित मूल्य सी॰ए॰पी॰एम॰ मूल्यांकन से अधिक है तो संपत्ति सस्ती है (यदि अनुमानित मूल्य सी॰ए॰पी॰एम॰ मूल्यांकन से कम है तो संपत्ति मंहगी है)।[४]
किसी परिसंपत्ति का प्रतिभूति बाजार रेखा पर स्थित नहीं होना उसके मूल्य में विसंगति को दर्शाता है। चूँकि समयबिंदु <math>t</math> पर संपत्ति का प्रत्याशित प्रतिफल <math>E(R_t)=\frac{E(P_{t+1})-P_t}{P_t}</math> जो कि सीएपीम द्वारा सुझाए प्रतिफल से अधिक है, तो इसका अर्थ है कि <math>P_t</math> बहुत कम है(the asset is currently undervalued), assuming that at time <math>t+1</math> the asset returns to the CAPM suggested price.[५]
सी॰ए॰पी॰एम॰ (जिसे कभी कभी certainty equivalent pricing formula भी कहा जाता है) का प्रयोग करने पर परिसंपत्ति का मूल्य <math>P_0</math>, निम्न लीनियर संबंध से प्रदर्शित किया जा सकता है:
- <math>P_0 = \frac{1}{1 + R_f} \left[E(P_T) - \frac{\mathrm{Cov}(P_T,R_M)(E(R_M) - R_f)}{\mathrm{Var}(R_M)}\right]</math>
जहाँ <math>P_T</math> संपत्ति या पोर्टफोलियो का payoff है।[४]
किसी विशिष्ट परिसम्पत्ति पर अपेक्षित वापसी
सी॰ए॰पी॰एम॰ द्वारा पता लगाया जा सकता है कि किसी विशिष्ट संपत्ति के तुलनात्मक जोखिम को ध्यान में रखते हुए उसकी अपेक्षित वापसी अर्थात् समायोजन दर (अर्थात् वह दर जिस पर कि उस संपत्ति के द्वारा भविष्य में पैदा होने वाली नकदी को समायोजित किया जाए), कितनी होनी चाहिए। यदि बीटा का मान एक से अधिक हो तो इसका अर्थ है - औसत से अधिक जोखिम; एक से कम का अर्थ है - औसत से कम जोखिम। इस प्रकार, किसी ज्यादा जोखिम वाले स्टॉक का बीटा अधिक होगा और उन्हें अधिक दर पर समायोजित किया जाएगा। जबकि कम संवेदनशील स्टॉक्स का बीटा कम होगा और उन्हें कम दर पर समायोजित किया जाएगा। यह प्रचलित अनौपचारिक धारणा, कि अधिक जोखिम लेने वाले निवेशक अधिक प्रतिफल की इच्छा रखते हैं, के अनुरूप ही है।
क्योंकि बीटा किसी एक परिसंपत्ति के जोखिम की पूरे बाजार जोखिम (अशाखनीय) के प्रति संवेदनशीलता का पैमाना (अनुपात) है, तो परिभाषा से स्पष्ट है कि बाजार जोखिम का बीटा का माप होगा : 1। बाजार जोखिम मापने के लिए एक पूरक पैमाने के रूप में स्टॉक मार्केट इंडेक्स का प्रयोग बहुतायत में किया जाता है, अतः इनका बीटा माप 1 होता है। इस प्रकार, एक बड़े और सुविशाखित पोर्टफोलियो (जैसे कि म्यूचुअल फंड) के निवेशक अपने निवेश से बाजार की चाल के अनुसार ही परिणामों की अपेक्षा कर सकते हैं।
जोख़िम एवं विशाखन
किसी भी पोर्टफोलियो में मौजूद जोखिम प्रमुखतः दो प्रकार के जोखिमों का योग होता है - व्यवस्थात्मक जोखिम, जिसे बाजार जोखिम या अशाखनीय जोखिम (undiversifiable risk) भी कहा जाता है, तथा अव्यवस्थात्मक जोखिम जिसे शाखनीय जोखिम कहा जाता है। व्यवस्थात्मक या बाजार जोखिम उन कारणों की वजह से होता है जो समस्त निवेश विकल्पों अर्थात पूरे बाजार को प्रभावित करते है। इस प्रकार के जोखिम पर नियंत्रण करना कठिन है। अव्यवस्थात्मक जोखिम वह जोखिम है जो किसी विशेष प्रतिभूति अथवा निवेश विकल्प को प्रभावित करता है। निवेश का विशाखन (डाइवर्सिफिकेशन- एक ही विकल्प में सारा निवेश न कर के भिन्न भिन्न विकल्पों में निवेश करना) करके ऐसे जोखिम को नियंत्रित किया जा सकता है।
A rational investor should not take on any diversifiable risk, as only non-diversifiable risks are rewarded within the scope of this model. Therefore, the required return on an asset, that is, the return that compensates for risk taken, must be linked to its riskiness in a portfolio context—i.e. its contribution to overall portfolio riskiness—as opposed to its "stand alone risk." In the CAPM context, portfolio risk is represented by higher variance i.e. less predictability. In other words the beta of the portfolio is the defining factor in rewarding the systematic exposure taken by an investor.
प्रभावी सीमांत क्षेत्र
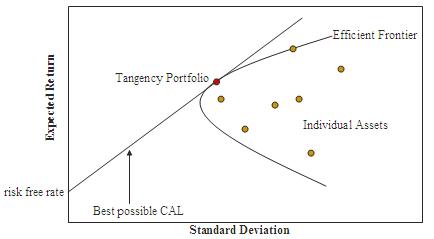
सी॰ए॰पी॰एम॰ मानता है कि किसी निवेश के जोखिम-प्रतिफल अनुपात को दुरुस्त किया जा सकता है, एक आदर्श (ऑप्टिमम) पोर्टफोलियो वह होगा जो कि एक निर्धारित प्रतिफल दर के लिए न्यूनतम जोखिम के साथ हो। इसके अतिरिक्त, क्योंकि पोर्टफोलियो में जुड़ने वाली हर नई संपत्ति पोर्टफोलियो का और विशाखन करती है, since each additional asset introduced into a portfolio further diversifies the portfolio, the optimal portfolio must comprise every asset, (assuming no trading costs) with each asset value-weighted to achieve the above (assuming that any asset is infinitely divisible). All such optimal portfolios, i.e., one for each level of return, comprise the efficient frontier.
Because the unsystematic risk is diversifiable, the total risk of a portfolio can be viewed as beta.
बाजार पोर्टफोलियो
कोई निवेशक एसा भी कर सकता है कि वह अपनी निधि का कुछ हिस्सा तो जोखिमयुक्त संपत्तियों में निवेश करे तथा कुछ हिस्सा नकद बचाकर रखे, जिसे जोखिम रहित दर पर कमाई होती रहे। (या फिर उधार लेकर जोखिमयु्क्त संपत्तियों में निवेश करे, जिस स्थिति में there is a negative cash weighting)। यहाँ पर जोखिमयुक्त व जोखिममुक्त का अनुपात overall return को निर्धारित नहीं करता - यह संबंध निश्चित ही linear है। इस प्रकार से यह संभव है कि निम्न दों में से किसी एक प्रकार एक निश्चित return प्राप्त किया जा सकता है :
- समस्त निधि को जोखिमयुक्त पोर्टफोलियो में निवेश करके
- या निधि का कुछ हिस्सा जोखिमयुक्त संपत्तियों में निवेश करके तथा बाकी हिस्सा नकद (या तो उधार लिया हुआ या निवेशित)
हालाँकि एक निश्चित प्रतिलाभ के लिए, उपरोक्त में से कोई एक विकल्प ही कुशल (optimal) सिद्ध होगा (न्यूनतम जोखिम को ध्यान में रखते हुए)। चूँकि जोखिममुक्त संपत्ति परिभाषतः किसी भी अन्य संपत्ति से correlated नहीं है, द्वितीय विकल्प में सामान्यतः कम विचलन (variance) होगा जिसके कारण यह दोनों में से अधिक कुशल होगा।
यह संबंध प्रभावी सीमा (the efficient frontier) पर स्थित अन्य पोर्टफोलिओज़ के लिए भी सही होगा : उच्च प्रतिलाभ के साथ कुछ नकद- अधिक कुशल है बजाय - उसी प्रतिलाभ दर पर मात्र निम्न प्रतिलाभ वाले पोर्टफोलियो के। एक निश्चित जोखिममुक्त दर के लिए, एक ही कुशल पोर्टफोलियो होगा जिसे कि नकदी के साथ मिलाकर किसी भी प्रतिलाभ के लिए न्यूनतम जोखिम की स्थिति प्राप्त की जा सकती है। यही मार्केट पोर्टफोलियो है।
सी॰ए॰पी॰एम॰ के अभिगृहीत
सभी निवेशकों:[६]
- का उद्देश्य आर्थिक उपयोगिताओं अधिकतम करना
- तर्कसंगत और जोखिम रहित हों
- निवेश की श्रेणि मोटे तौर पर विविध हो
- कीमत क्रय योग्य हो, जैसे, वो कीमतों को प्रभावित करने वाले ना हों।
- ब्याज की जोखिम रहित दर के तहत असीमित मात्रा में उधार देने और उधार लेने में सक्षम हो सकें।
- लेन-देन या कराधान लागत रहित व्यापार
- लघु पार्सल में निहायत विभाज्य प्रतिभूतियों के साथ विभाजित हों।
- सभी निवेशकों को एक ही समय में सभी सुचनाएँ उपलब्ध करवाना।
सी॰ए॰पी॰एम॰ में समस्या
- यह मॉडल मानता है कि विवरणियों में अन्तर जोख़िम का एक पर्याप्त मापन है। इसमें यह पूर्वधारणा निहित होती है कि विवरणियां प्रसामान्य रूप से वितरित होती हैं अथवा यथार्थ में द्वि-प्राचल शैली में वितरित होती हैं लेकिन समान्य विवरणी वितरण के लिए अन्य जोख़िम मापन (जैसे संगत जोखिम माप) सक्रिय और सम्भावित शेयरधारक वरीयताएँ अधिक पर्याप्त रूप से प्रतिबिंबित करता है। वास्तव में वित्तीय निवेश में जोखिम अपने आप में भिन्नता के साथ नहीं होती बल्कि यहाँ पिछड़ने की प्रायिकता है: यह प्रकृति में असममित है। बार्कलेज वेल्थ द्वारा "असामान्य प्रतिफल वाली परिसम्पत्तियो के आबंटन" विषय पर प्रकाशित एक अनुसन्धान में पाया गया कि अत्यल्प जोखिम क्षमता वाले निवेशकों को इससे कहीं अधिक मात्र में नकदी रखनी चाहिए जितने कि इस मॉडल द्वारा बताई जाती है।[७]
- यह मॉडल मानता है कि सक्रिय एवं भावी शेयरधारकों के संभाव्यता अनुमान वास्तविक प्रतिफल से मेल खाते हैं। एक अन्य संभावना यह भी है कि सक्रिय एवं भावी शेयरधारकों के अनुमान अथवा आशाएँ biased हों, जिससे कि बाजार मूल्य informationally inefficient हो जाएगा. इस सम्भावना का अध्ययन वित्त की एक शाखा व्यावहारिक वित्त के अंतर्गत किया जाता है जिसमें सी ए पी एम के विकल्प के तौर पर मनोवैज्ञानिक मान्यताओं को प्रयोग में लिया जाता है जैसे कि केंट डेनियल, डेविड हिर्श्लेइफ़ेर व् अवनीधर सुब्रह्मण्यम का " अतिविश्वास आधारित परिसंपत्ति मूल्य निर्धारण मॉडल (2001).[८]
- थ्योरी के अनुसार मार्केट पोर्टफोलियो में निवेशक की सभी तरह की संपत्तियाँ शामिल होनी चाहिएँ जिनमें कि कलाकृतियाँ, जायदाद, मानव-पूँजी आदि भी। किंतु वास्तविकता में यह सब देखना संभव नहीं होता और लोग प्रायः किसी स्टॉक इण्डेक्स को "सच्चे मार्केट पोर्टफोलियो" के विकल्प के तौर पर प्रयोग करते हैं। हालाँकि यह सिद्ध किया जा चुका है कि यह अदला बदली innocuous नहीं है तथा इससे सी॰ए॰पी॰एम॰ की वैधता के बारे में गलत परिणाम निकल सकते हैं। और यह भी कहा गया है कि "सच्चे मार्केट पोर्टफोलियो" को पूरी तरह से ना देख पाने के चलते, सी॰ए॰पी॰एम॰ को empirically testable नहीं माना जा सकता। इस विचार का प्रतिपादन विस्तार में रिचर्ड रॉल द्वारा 1977 के एक पेपर में किया गया, जिसे सामान्यतः रॉल की आलोचना कहा जाता है।.[९]
- यह मॉडल मानता है कि economic agents optimise over a short-term horizon, and in fact investors with longer-term outlooks would optimally choose long-term inflation-linked bonds instead of short-term rates as this would be more risk-free asset to such an agent.[१०][११]
- यह मॉडल मात्र दो तिथियाँ मानता है जिससे कि पोर्टफोलियो को consume व समय समय पर पुनर्संतुलित करने की कोई संभावना नहीं बचती। इस मॉडल के आधारभूत insights का विस्तारित व सामान्यकरण (सार्वभौमीकरण, generalisation) किया गया है रॉबर्ट मर्टन के intertemporal CAPM (ICAPM),[१२] तथा डगलस ब्रीडन व मार्क रुबिंस्टीन के consumption CAPM (CCAPM) में।[१३]
- यह मॉडल मानता है कि सभी सक्रिय एवं भावी शेयरधारक/निवेशक अपनी समस्त संपत्तियों को मात्र एक पोर्टफोलियो में एक साथ consider करते हुए उसी पोर्टफोलियो को optimize करेंगे। जबकि यह वास्तविकता से बहुत अलग है जहाँ कि निवेशक कई टुकड़ों में, अथवा कई बार तो अलग अलग लक्ष्यों के लिए अलग अलग पोर्टफोलियो रखते हैं— देखें व्यवहारिक पोर्टफोलियो थ्योरी[१४] तथा मास्लोवियन पोर्टफोलियो थ्योरी।[१५]
- Empirical tests दिखाते हैं कि बाजार की विसंगतियाँ जैसे कि मात्रा व कीमत प्रभाव (size and value effect) की व्याख्या सी॰ए॰पी॰एम॰ से नहीं की जा सकती।[१६] For details see the Fama–French three-factor model.[१७]
सी॰ए॰पी॰एम॰ का विकल्प: द्वि-बीटा
द्वि-बीटा मॉडल उर्ध्वगामी बीटा को अधिगामी बीटा से भिन्न करता है। सी॰ए॰पी॰एम॰ तथा द्वि-बीटा मॉडल में अंतर यह है कि सी॰ए॰पी॰एम॰ मॉडल की मान्यता है कि उर्ध्वगामी औेर अधिगामी बीटा एक ही हैं जबकि द्वि-बीटा मॉडल एसा नहीं मानता। एसी मान्यता कभी विरले ही ठीक होती है, अतः द्वि-बीटा मॉडल को ही अधिक उपयुक्त माना जाता है।सन्दर्भ त्रुटि: अमान्य <ref> टैग;
(संभवतः कई) अमान्य नाम
इन्हें भी देखें
- उपभोग आधारित पूँजी परिसंपत्ति कीमत निर्धारण मॉडल (CCAPM)
- कम जोखिम
- प्रभावी बाजार परिकल्पना
- en:Financial risk
- en:Hamada's equation
- en:Macro risk
- en:Risk management tools
- en:Single-index model
- en:Upside risk
- en:Valuation (finance)
सन्दर्भ
- ↑ अ आ इ साँचा:cite web
- ↑ साँचा:cite journal
- ↑ साँचा:cite journal
- ↑ अ आ साँचा:cite book
- ↑ साँचा:cite book
- ↑ साँचा:cite book
- ↑ स्क्रिप्ट त्रुटि: "citation/CS1" ऐसा कोई मॉड्यूल नहीं है।
- ↑ साँचा:cite journal
- ↑ साँचा:cite journal
- ↑ स्क्रिप्ट त्रुटि: "citation/CS1" ऐसा कोई मॉड्यूल नहीं है।
- ↑ Campbell, J & Vicera, M "Strategic Asset Allocation: Portfolio Choice for Long Term Investors". Clarendon Lectures in Economics, 2002. ISBN 978-0-19-829694-2
- ↑ साँचा:cite journal
- ↑ साँचा:cite journal
- ↑ साँचा:cite journal
- ↑ साँचा:cite journal
- ↑ Fama, Eugene F.; French, Kenneth R. (1993). "Common Risk Factors in the Returns on Stocks and Bonds". Journal of Financial Economics. 33 (1): 3–56. doi:10.1016/0304-405X(93)90023-5.
- ↑ Fama, Eugene F.; French, Kenneth R. (1992). "The Cross-Section of Expected Stock Returns". Journal of Finance. 47 (2): 427–465. doi:10.2307/2329112.
ग्रंथसूची
- Black, Fischer., Michael C. Jensen, and Myron Scholes (1972). The Capital Asset Pricing Model: Some Empirical Tests, pp. 79–121 in M. Jensen ed., Studies in the Theory of Capital Markets. New York: Praeger Publishers.
- Fama, Eugene F. (1968). Risk, Return and Equilibrium: Some Clarifying Comments. Journal of Finance Vol. 23, No. 1, pp. 29–40.
- Fama, Eugene F. and Kenneth French (1992). The Cross-Section of Expected Stock Returns. Journal of Finance, June 1992, 427–466.
- French, Craig W. (2003). The Treynor Capital Asset Pricing Model, Journal of Investment Management, Vol. 1, No. 2, pp. 60–72. Available at https://web.archive.org/web/20150906033844/https://www.joim.com/
- French, Craig W. (2002). Jack Treynor's 'Toward a Theory of Market Value of Risky Assets' (December). Available at https://web.archive.org/web/20200602161804/https://papers.ssrn.com/sol3/papers.cfm?abstract_id=628187
- Lintner, John (1965). The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets, Review of Economics and Statistics, 47 (1), 13–37.
- Markowitz, Harry M. (1999). The early history of portfolio theory: 1600–1960, Financial Analysts Journal, Vol. 55, No. 4
- Mehrling, Perry (2005). Fischer Black and the Revolutionary Idea of Finance. Hoboken: John Wiley & Sons, Inc.
- Mossin, Jan. (1966). Equilibrium in a Capital Asset Market, Econometrica, Vol. 34, No. 4, pp. 768–783.
- Ross, Stephen A. (1977). The Capital Asset Pricing Model (CAPM), Short-sale Restrictions and Related Issues, Journal of Finance, 32 (177)
- Rubinstein, Mark (2006). A History of the Theory of Investments. Hoboken: John Wiley & Sons, Inc.
- Sharpe, William F. (1964). Capital asset prices: A theory of market equilibrium under conditions of risk, Journal of Finance, 19 (3), 425–442
- Stone, Bernell K. (1970) Risk, Return, and Equilibrium: A General Single-Period Theory of Asset Selection and Capital-Market Equilibrium. Cambridge: MIT Press.
- Tobin, James (1958). Liquidity preference as behavior towards risk, The Review of Economic Studies, 25
- Treynor, Jack L. (1961). Market Value, Time, and Risk. Unpublished manuscript.
- Treynor, Jack L. (1962). Toward a Theory of Market Value of Risky Assets. Unpublished manuscript. A final version was published in 1999, in Asset Pricing and Portfolio Performance: Models, Strategy and Performance Metrics. Robert A. Korajczyk (editor) London: Risk Books, pp. 15–22.
- Mullins, David W. (1982). Does the capital asset pricing model work?, Harvard Business Review, January–February 1982, 105–113.
बाहरी कड़ियाँ
- ऑनलाइन बैंकिंग शब्दावली, भारतीय रिज़र्व बैंक की वैबसाईट पर
- MacroRisk Analytics “Patented and proprietary macro risk measurements and tools for investors since 1999”.
- Joshua Kennon "Thoughts on Business, Politics & Life from a Private Investor".
- Stockmarket Software and Education
- Multiasset efficient frontier
