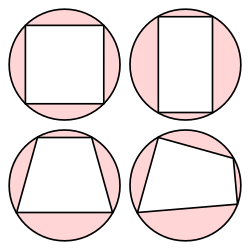
चक्रीय चतुर्भुज
2409:4064:221d:dc5f::16c4:d0ac (चर्चा) द्वारा परिवर्तित ११:०१, १८ दिसम्बर २०२० का अवतरण
चक्रीय चतुर्भुज (cyclic quadrilateral) ऐसे चतुर्भुज को कहते हैं जिसके चारो शीर्ष किसी वृत्त की परिधि पर स्थित हों। किसी चक्रीय चतुर्भुज के आमने-सामने के कोणों का योग 180 होता है।
क्षेत्रफल
यदि सभी भुजाएँ दी गयी हों तो चक्रीय चतुर्भुज का क्षेत्रफल, ब्रह्मगुप्त सूत्र से निकाला जाता है।
- <math>\sqrt{(s-a)(s-b)(s-c)(s-d)} \, </math>
जहाँ s, अर्धपरिधि है।
<math>s=\frac{a+b+c+d}{2}</math>
अन्य गुण
| चक्रीय चतुर्भुज के गुणधर्म | ||
|---|---|---|
| क्षेत्रफल | <math>A \, = \, \sqrt{(s-a) (s-b) (s-c) (s-d)}</math> | |
| क्षेत्रफल | <math>A \, = \, \frac{e \cdot (ab+cd)}{4R}
= \frac{f \cdot (ad+bc)}{4R}</math> | |
| भुजाओं की लंबाई | <math>a,\,b,\,c,\,d</math> | |
| अर्धपरिधि | <math>s \, = \, \frac{a+b+c+d}{2}</math> | |
| विकर्ण | <math>e = \overline{AC}=\sqrt{\frac{(ac+bd)(ad+bc)}{ab+cd}}\, \, f=\overline{BD}=\sqrt{\frac{(ab+cd)(ac+bd)}{ad+bc}} </math> | |
| परिवृत्त की त्रिज्या | <math>R=\frac{1}{4A}\sqrt{(ab+cd)(ac+bd)(ad+bc)},</math> | |
इन्हें भी देखें
- ब्रह्मगुप्त का सूत्र - चक्रीय चतुर्भुज के क्षेत्रफल की गणना के लिए
- ब्रह्मगुप्त प्रमेय - चक्रीय चतुर्भुज के एक विशेष गुण से सम्बन्धित