लजान्द्र बहुपद

<math>{d \over dx} \left[ (1-x^2) {d \over dx} P_n(x) \right] + n(n+1)P_n(x) = 0.</math>

यह नामकरण आद्रियें मारि लजान्द्र‎ के नाम पर किया गया है। ये बहुपद लांबिक फलन (आर्थोगोनल फलन) के सरलतम उदाहरण हैं।

कुछ लजान्द्र बहुपद

आरम्भ के ग्यारह लजान्द्र बहुपद नीचे दिए गए हैं:

n	<math>P_n(x)\,</math>
0	<math>1\,</math>
1	<math>x\,</math>
2	<math>\begin{matrix}\frac12\end{matrix} (3x^2-1) \,</math>
3	<math>\begin{matrix}\frac12\end{matrix} (5x^3-3x) \,</math>
4	<math>\begin{matrix}\frac18\end{matrix} (35x^4-30x^2+3)\,</math>
5	<math>\begin{matrix}\frac18\end{matrix} (63x^5-70x^3+15x)\,</math>
6	<math>\begin{matrix}\frac1{16}\end{matrix} (231x^6-315x^4+105x^2-5)\,</math>
7	<math>\begin{matrix}\frac1{16}\end{matrix} (429x^7-693x^5+315x^3-35x)\,</math>
8	<math>\begin{matrix}\frac1{128}\end{matrix} (6435x^8-12012x^6+6930x^4-1260x^2+35)\,</math>
9	<math>\begin{matrix}\frac1{128}\end{matrix} (12155x^9-25740x^7+18018x^5-4620x^3+315x)\,</math>
10	<math>\begin{matrix}\frac1{256}\end{matrix} (46189x^{10}-109395x^8+90090x^6-30030x^4+3465x^2-63)\,</math>

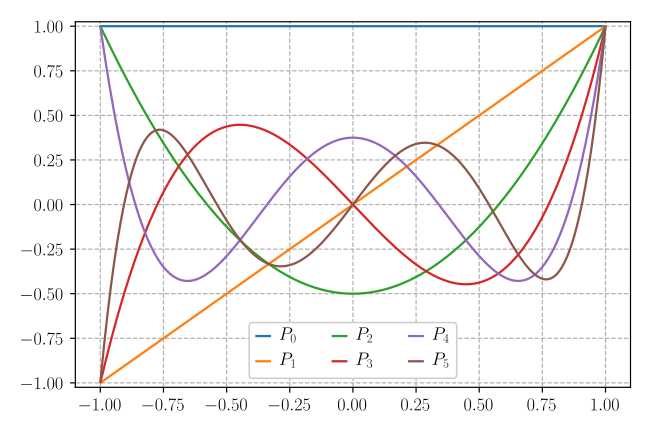
नीचे के चित्र में n=5 तक के लजान्द्र बहुपदों का आरेख (ग्राफ) दिखाया गया है।