जड़त्वाघूर्ण

रस्सी पर करतब दिखाने वाला नट रस्सी पर संतुलन बनाये रखने के लिए एक लम्बी लाठी (रॉड) का प्रयोग करता है। इसके कारण लाठी सहित उसका जडत्वाघूर्ण बहुत अधिक हो जाता है और चलते समय उत्पन्न थोड़े-थोड़े असंतुलित बलों को आसानी से संतुलित कर लेता है।

किसी पिण्ड की घूर्णन की दर के परिवर्तन के प्रति प्रतिरोध की माप उस पिण्ड का जड़त्वाघूर्ण (Moment of inertia) कहलाता है। किसी पिण्ड का जड़त्वाघूर्ण उसके आकार-प्रकार एवं उसके अन्दर द्रव्यमान के वितरण की प्रकृति पर निर्भर करता है। स्थानान्तरण गति में जो कार्य द्रव्यमान का है वही कार्य घूर्णन गति में जड़त्वाघूर्ण का होता है। जड़त्वाघूर्ण के प्रतीक के लिये I या कभी-कभी J का प्रयोग किया जाता है। जड़त्वाघूर्ण की अवधारणा का उल्लेख सबसे पहले यूलर (Euler) ने सन् १७३० में अपनी पुस्तक ' Theoria motus corporum solidorum seu rigidorum ' में किया था।

परिभाषा

कुछ पिण्डों के जड़त्वाघूर्ण

किसी स्थिर अक्ष के परितः कणों के किसी निकाय का जड़त्वाघूर्ण J_a, उन सभी कणों के द्रव्यमान तथा उनकी अक्ष से दूरी के वर्ग के गुणनफलों के योग के बराबर होता है।

<math>J_a=\sum_{i=1}^n m_i r_i^2\,\!</math>,

जहाँ:

• m_i — i-वें कण का द्रव्यमान
• r_i — i-वें कण की अक्ष से लम्बवत दूर

कुछ पिण्डों के मुख्य जड़त्वाघूर्ण

पिण्ड	व्याख्या	जड़त्वाघूर्ण
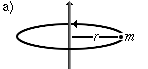
	Eine Punktmasse im Abstand <math>r</math> um eine Drehachse.	<math>J = m \cdot r^2</math>
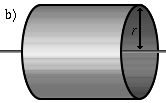
	Ein Zylindermantel, der um seine Symmetrieachse rotiert, für eine Wandstärke <math>\scriptstyle d \ll r</math>.	<math>J \approx m \cdot r^2</math>
	Ein Vollzylinder, der um seine Symmetrieachse rotiert.	<math>J = {1 \over 2} m \cdot r^2</math>
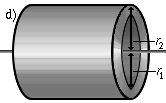
	Ein Hohlzylinder, der um seine Symmetrieachse rotiert. Schließt die vorgenannten Grenzfälle Zylindermantel und Vollzylinder mit ein.	<math>J = m \frac{r_1^2+r_2^2}{2}</math>
	Ein Vollzylinder, der um eine Querachse (zweizählige Symmetrieachse) rotiert.	<math>J = {1 \over 4} m \cdot r^2 + {1 \over 12} m \cdot l^2</math>
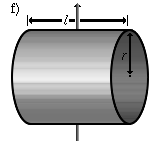
	Ein Zylindermantel, der um eine Querachse (zweizählige Symmetrieachse) rotiert.	<math>J = {1 \over 2} m \cdot r^2 + {1 \over 12} m \cdot l^2</math>
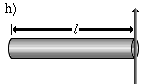
	Ein dünner Stab, der um eine Querachse (zweizählige Symmetrieachse) rotiert. Diese Formel ist eine Näherung für einen Zylinder mit <math>\scriptstyle r\ll l</math>.	<math>J = {1 \over 12} m \cdot l^2</math>
	Dünner Stab, der um eine Querachse durch ein Ende rotiert. Diese Formel ist die Anwendung der Steiner-Regel auf den dünnen Stab.	<math>J = {1 \over 3} m \cdot l^2</math>
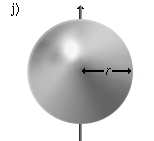
	Eine Kugelschale, die um eine Achse durch den Mittelpunkt rotiert, für eine Wandstärke <math>\scriptstyle d \ll r</math>.	<math>J \approx {2 \over 3} m \cdot r^2</math>
	Eine massive Kugel, die um eine Achse durch den Mittelpunkt rotiert.	<math>J = {2 \over 5} m \cdot r^2</math>
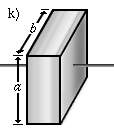
	Ein Quader, der um eine Achse durch den Mittelpunkt rotiert, die parallel zu seinen Kanten c liegt.	<math>J = {1 \over 12} m \cdot (a^2 + b^2)</math>
	Ein massiver Kegel, der um seine Achse rotiert.	<math>J = {3 \over 10} m \cdot r^2</math>
	Ein Kegelmantel, der um seine Achse rotiert. Die Gleichheit mit dem Trägheitsmoment eines Vollzylinders kann man sich so vorstellen, dass man jeden Kegelmantel zu einer Kreisscheibe „plattdrücken“ kann, ohne sein Trägheitsmoment zu verändern.	<math>J = {1 \over 2} m \cdot r^2</math>
	Ein massiver Kegelstumpf, der um seine Achse rotiert.	<math>J = {3 \over 10} m \cdot { (r_1^5 - r_2^5)\over (r_1^3 - r_2^3) }</math>
	Eine vierseitige, regelmäßige, massive Pyramide, die um ihre Symmetrieachse rotiert.	<math>J = {1 \over 5} m \cdot r^2 = \frac{1}{10}m l^2</math>
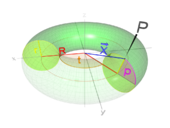
	Volltorus mit dem Radius <math>R</math> (rot) und der halben Dicke <math>r</math> (gelb), der um die Symmetrieachse rotiert. (Der Radius <math>R</math> ist so gemeint, dass der Außenradius des Torus <math>R+r</math> ergibt)	<math>J = m \left (\frac{3}{4} \cdot r^2+R^2 \right)</math>

इन्हें भी देखें

किसी नत समतल से बिना फिसले लुढ़कती हुई चार वस्तुएँ - खोखला गोला (लाल) , ठोस गोला (नारंगी), बेलनाकार छल्ला (हरा), ठोस बेलन (नीला)। इनके द्वारा समाप्ति-रेखा तक पहुँचने में लिया गया समय इनके जड़त्वाघूर्ण पर निर्भर करता है।

• जड़त्वाघूर्णों की सूची
• समान्तर अक्ष का प्रमेय
• लम्बवत अक्ष का प्रमेय
• क्षेत्रफल का द्वितीय आघूर्ण
• संहति केन्द्र (सेन्टर ऑफ मास)
• कोणीय संवेग

बाहरी कड़ियाँ

• Angular momentum and rigid-body rotation in two and three dimensions
• Lecture notes on rigid-body rotation and moments of inertia
• The moment of inertia tensor
• An introductory lesson on moment of inertia: keeping a vertical pole not falling down (Java simulation)
• Tutorial on finding moments of inertia, with problems and solutions on various basic shapes
• Measuring moment of inertia