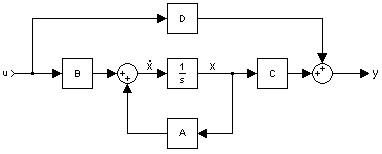
अवस्था-समष्टि
साँचा:asbox अवस्था-समष्टि निरूपण (state space representation), गतिकीय तन्त्रों के कई प्रकार के निरूपणों में से एक है। वस्तुतः यह समय-क्षेत्र निरूपण ( time domain representation) है और बहु-इनपुट तथा बहु-आउटपुट (MIMO) गतिक तंत्रों के नियन्त्रण से सम्बन्धित विवेचन के लिये विशेष रूप से उपयोगी है। इसके अलावा यह अरैखिक तंत्रों और काल-परिवर्ती तंत्रों (time-variable systems) के विश्लेषण तथा संश्लेषण के लिये भी उपयोगी है। तंत्रों के निरूपण की इस पद्धति में तंत्र के अवस्था चरों (state variables), इनपुट तथा आउटपुट को प्रथम क्रम (फर्स्ट ऑर्डर) के अवकल समीकरणों द्वारा निरूपित किया जाता है। अवस्था क्षेत्र मोडेल में दो समीकरण होते हैं - अवस्था समीकरण तथा आउटपुट समीकरण।
लाभ एवं उपयोग
आवृत्ति-क्षेत्र निरूपण की तुलना में अवस्था-समष्टि निरूपण के निम्नलिखित लाभ हैं-
- (१) यह तंत्र को एक लघु (compact) तथा सुविधाजनक रूप में प्रस्तुत करता है।
- (२) MIMO तंत्रों के लिये विशेष उपयोगी है।
- (३) p-इन्पुट तथा q-आउटपुट वाले किसी अपरिवर्ती रैखिक तंत्र को s-डोमेन में निरूपित करने के लिये pq ट्रांसफर फलनों की आवश्यकता होगी जबकि अवस्था-क्षेत्र में उसे ही निरूपित करने के लिये केवल दो मैट्रिक्स लगते हैं।
- (४) आवृत्ति-डोमेन में केवल उन्हीं तंत्रों को निरूपित किया जा सकता है जो रैखिक हों तथा उनकी आरम्भिक अवस्थायें शून्य (initial conditions) हों। अवस्था-क्षेत्र में निरूपण के लिये यह बिलकुल आवश्यक नहीं है।
- (५) स्टेट-स्पेस मॉडल, कम्प्यूटर द्वारा विश्लेषण तथा अध्ययन के लिये विशेष रूप से उपयोगी है।
'अवस्था क्षेत्र' या स्टेट-स्पेस एक काल्पनिक क्षेत्र है जिसके अक्ष अवस्था-चर हैं। इस स्पेस में तंत्र के अवस्था चरों को एक वेक्टर के रूप में देखा जा सकता है।
रैखिक तंत्र
किसी p इनपुट, q आउटपुट तथा n अवस्था-चरों से युक्त तंत्र को इस पद्धति में निम्नलिखित प्रकार से निरूपित किया जाता है:
- <math>\dot{\mathbf{x}}(t) = A(t) \mathbf{x}(t) + B(t) \mathbf{u}(t)</math>
- <math>\mathbf{y}(t) = C(t) \mathbf{x}(t) + D(t) \mathbf{u}(t)</math>
जहाँ
- <math>x(t) \in \mathbb{R}^n</math>; <math>y(t) \in \mathbb{R}^q</math>; <math>u(t) \in \mathbb{R}^p</math>;
- <math>\operatorname{dim}[A(\cdot)] = n \times n</math>,
- <math>\operatorname{dim}[B(\cdot)] = n \times p</math>,
- <math>\operatorname{dim}[C(\cdot)] = q \times n</math>,
- <math>\operatorname{dim}[D(\cdot)] = q \times p</math>,
- <math>\dot{\mathbf{x}}(t) := {d\mathbf{x}(t) \over dt}</math>.
called state vector, and (\ cdot) is called output vector, u (\ cdot) is called input vector (or control), A (\ cdot) is the parent of states, B (\ cdot) is the input matrix, C (\ cdot) is the output matrix and D (\ cdot)
- <math>x(\cdot)</math> को अवस्था सदिश (स्टेट वेक्टर) कहते हैं,
- <math>y(\cdot)</math> को आउटपुट सदिश कहते हैं,
- <math>u(\cdot)</math> को इनपुट वेक्टर (या कन्ट्रोल वेक्तर) कहते है,
- <math>A(\cdot)</math> को अवस्था मैट्रिक्स कहते हैं,
- <math>B(\cdot)</math> को इनपुट मैट्रिक्स कहते हैं,
- <math>C(\cdot)</math> को आउटपुट मैट्रिक्स कहते हैं, तथा
- <math>D(\cdot)</math> को फीडफॉरवर्ड मैट्रिक्स कहते हैं।
- <math>\dot{\mathbf{x}}(t) := \frac{\operatorname{d}}{\operatorname{d}t} \mathbf{x}(t)</math>.
उपरोक्त निरूपण में सभी मैट्रिक्स समय के साथ परिवर्ती हो सकते हैं (इसका अर्थ है कि तंत्र के अवयवों का मान समय के साथ परिवर्ती है।) किन्तु यदि तंत्र रैखिक तथा समय के साथ अपरिवर्ती हो (LTI system) तो ये मैट्रिक्स अपरिवर्ती होंगे। चर समय <math>t</math> सतत हो सकता है (उदाहरणार्थ <math>t \in \mathbb{R}</math>) या विविक्त (discrete) (e.g. <math>t \in \mathbb{Z}</math>)। इस स्थिति में समय <math>t</math> के बजाय प्रायः चर <math>k</math> का प्रयोग किया जाता है। जिन तंत्रों में सतत परिवर्ती तथा विविक्त रूप से परिवर्तित होने वाले अवयव होते हैं उनको संकर (Hybrid) तंत्र कहते हैं। अतः विभिन्न स्थितियों में स्टेट-स्पेस मॉडल का रूप निम्नलिखित प्रकार का होगा:
| System type | स्टेट स्पेस मॉडल |
| Continuous time-invariant | <math>\dot{\mathbf{x}}(t) = A \mathbf{x}(t) + B \mathbf{u}(t)</math> <math>\mathbf{y}(t) = C \mathbf{x}(t) + D \mathbf{u}(t)</math> |
| Continuous time-variant | <math>\dot{\mathbf{x}}(t) = \mathbf{A}(t) \mathbf{x}(t) + \mathbf{B}(t) \mathbf{u}(t)</math> <math>\mathbf{y}(t) = \mathbf{C}(t) \mathbf{x}(t) + \mathbf{D}(t) \mathbf{u}(t)</math> |
| Explicit discrete time-invariant | <math>\mathbf{x}(k+1) = A \mathbf{x}(k) + B \mathbf{u}(k)</math> <math>\mathbf{y}(k) = C \mathbf{x}(k) + D \mathbf{u}(k)</math> |
| Explicit discrete time-variant | <math>\mathbf{x}(k+1) = \mathbf{A}(k) \mathbf{x}(k) + \mathbf{B}(k) \mathbf{u}(k)</math> <math>\mathbf{y}(k) = \mathbf{C}(k) \mathbf{x}(k) + \mathbf{D}(k) \mathbf{u}(k)</math> |
| Laplace domain of continuous time-invariant |
<math>s \mathbf{X}(s) = A \mathbf{X}(s) + B \mathbf{U}(s)</math> <math>\mathbf{Y}(s) = C \mathbf{X}(s) + D \mathbf{U}(s)</math> |
| Z-domain of discrete time-invariant |
<math>z \mathbf{X}(z) = A \mathbf{X}(z) + B \mathbf{U}(z)</math> <math>\mathbf{Y}(z) = C \mathbf{X}(z) + D \mathbf{U}(z)</math> |
अवस्था समीकरण का समाकलन (इन्टीग्रेशन)
किसी तंत्र के अवस्था चर उसके पुराने (भूत) अवस्थाओं एवं इनपुटों से निर्धारित होते हैं। वस्तुतः यदि समयान्तराल [t_i, t_f ~] में पुराना स्टेट x (t_i) तथा इनपुट u (t) ज्ञात हों तो x (t_f) के मान की गणना की जा सकती है:
- <math> x(t_f) = x(t_i)e^{A(t_f-t_i)} + \int_{t_i}^{t_f}e^{A(t_f-\tau)}B u(\tau)d\tau </math>
नियंत्रणीयता तथा प्रेक्षणीयता
नियंत्रणियता
उस तंत्र को नियन्त्रणीय (कन्ट्रोलेबल) कहते हैं जिसको, स्वीकार्य इनपुटों के माध्यम से, किसी एक अवस्था से दूसरी अवस्था में सीमित समय में ले जाया जा सकता है। कोई सतत, काल-अपरिवर्ती, रैखिक अवस्था-मॉडल नियंत्रणीय (controllable) होगा यदि और केवल यदि-
- <math>\operatorname{rank}\begin{bmatrix}B& AB& A^{2}B& \dots & A^{n-1}B\end{bmatrix} = n, \,</math>
जहाँ 'रैंक' (rank) का अर्थ किसी मैट्रिक्स की रैखिक रूप से स्वतंत्र पंक्तियों की संख्या है।
प्रेक्षणीयता
वह तंत्र 'प्रेक्षणीय' (Observabe) कहलाता है जिसके आउटपुटों का ज्ञान होने पर उसके आन्तरिक अवस्थाओं की गणना की जा सके।
कोई सतत, काल-अपरिवर्ती, रैखिक अवस्था-मॉडल प्रेक्षणीय होगा, यदि और केवल यदि-
- <math>\operatorname{rank}\begin{bmatrix}C\\ CA\\ \vdots\\ CA^{n-1}\end{bmatrix} = n. \,</math>
उपरोक्त विवेचन का सारांश यह है कि नियन्त्रणियता का अर्थ यह है कि उस तंत्र को एक अवस्था से दूसरे अवस्था तक सीमित समय में ले जाने के लिये आवश्यक इन्पुट, सम्भव है। प्रेक्षणीयता का अर्थ यह है कि यदि किसी तंत्र के आउटपुट ज्ञात होने पर आनतरिक अवस्थाएं निकाली जा सकतीं हैं।
ट्रांसफर फलन से अवस्था-मॉडल
इन्हें भी देखें
- अवस्था प्रेक्षक (स्टेट ऑब्जर्वर)